Question

在平面直角坐标系中，已知向量

a

=(x，y-4)，

b

=(kx，y+4)（k∈R），

a

⊥

b

，动点M（x，y）的轨迹为T．
（1）求轨迹T的方程，并说明该方程表示的曲线的形状；
（2）当k=1时，已知O（0，0）、E（2，1），试探究是否存在这样的点Q：Q是轨迹T内部
的整点（平面内横、纵坐标均为整数的点称为整点），且△OEQ的面积S_△OEQ=2？
若存在，求出点Q的坐标；若不存在，说明理由．

Answer 1

分析：（1）根据

a

⊥

b

得到

a

•

b

=0可求关于动点M（x，y）的方程，由圆锥曲线的性质对k进行讨论即可．
（2）先确定轨迹T的方程，然后假设存在满足条件得点Q，联立直线方程和轨迹T的方程可得答案．

解答：解：（1）∵

a

⊥

b

∴

a

•b

=(x，y-4)•(kx，y+4)=0，
得kx²+y²-16=0，即kx²+y²=16
当k=0时，方程表示两条与x轴平行的直线；
当k=1时，方程表示以原点为圆心，4为半径的圆
当k＞0且k≠1时，方程表示椭圆；
当k＜0时，方程表示双曲线．

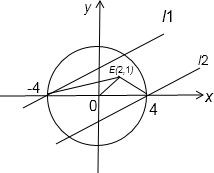（2）由（1）知，当k=1时，轨迹T的方程为：x²+y²=4²．
连接OE，易知轨迹T上有两个点A（-4，0），B（4，0）满足S_△OEA=S_△OEB=2，
分别过A、B作直线OE的两条平行线l₁、l₂．

∵同底等高的两个三角形的面积相等，
∴符合条件的点均在直线l₁、l₂上．
∵kOE=

1

2

，∴直线l₁、l₂的方程分别为：y=

1

2

(x+4)、y=

1

2

(x-4)
设点Q（x，y）（x，y∈Z）∵Q在轨迹T内，∴x²+y²＜16
分别解

x2+y2＜16 y= 1 2 (x+4)

与

x2+y2＜16 y= 1 2 (x-4)

得-4＜x＜2

2

5

与-2

2

5

＜x＜4
∵x，y∈Z∴x为偶数，在(-4，2

2

5

)上x=-2，，0，2，对应的y=1，2，3；
在(-2

2

5

，4)上x=-2，0，2，对应的y=-3，-2，-1
∴满足条件的点Q存在，共有6个，它们的坐标分别为：
（-2，1），（0，2），（2，3），（-2，-3），（0，-2），（2，-1）．

点评：本题主要考查向量的垂直和点乘之间的关系和圆锥曲线的有关问题．圆锥曲线每年必考，这种题型解题时经常是圆锥曲线和直线的联立来解决问题．