题目内容
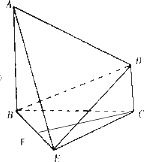 如图,已知AB⊥平面BCE,CD∥AB,△BCE是正三角形,AB=BC=2CD.
如图,已知AB⊥平面BCE,CD∥AB,△BCE是正三角形,AB=BC=2CD.(Ⅰ)若F是BE的中点,求证CF∥平面ADE;
(Ⅱ)求证:平面ADE⊥平面ABE;
分析:(Ⅰ)取BE的中点F、AE的中点G,连接FG,GD,CF
F是BE的中点,要证CF∥平面ADE,只需证明CF平行平面ADE内的直线GD即可.
(Ⅱ)要证平面ADE⊥平面ABE,只需证明平面ADE内的直线DG,垂直平面ABE即可.
F是BE的中点,要证CF∥平面ADE,只需证明CF平行平面ADE内的直线GD即可.
(Ⅱ)要证平面ADE⊥平面ABE,只需证明平面ADE内的直线DG,垂直平面ABE即可.
解答: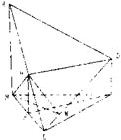 解:(Ⅰ)当F为BE的中点时,CF∥平面ADE(1分)
解:(Ⅰ)当F为BE的中点时,CF∥平面ADE(1分)
证明:取BE的中点F、AE的中点G,连接FG,GD,CF
∴GF=
AB,GF∥AB
∵DC=
AB,CD∥AB
∴CD∥GF CD=GF
∴CFGD是平行四边形(4分)
∴CD∥GD
∴CF∥平面ADE(6分)
(Ⅱ)∵CF⊥BF,CF⊥AB
∴CF⊥平面ABE(8分)
∵CF∥DG
∴DG⊥平面ABE(10分)
∵DG?平面ADE
∴平面ABE⊥平面ADE(12分)
 解:(Ⅰ)当F为BE的中点时,CF∥平面ADE(1分)
解:(Ⅰ)当F为BE的中点时,CF∥平面ADE(1分)证明:取BE的中点F、AE的中点G,连接FG,GD,CF
∴GF=
| 1 |
| 2 |
∵DC=
| 1 |
| 2 |
∴CD∥GF CD=GF
∴CFGD是平行四边形(4分)
∴CD∥GD
∴CF∥平面ADE(6分)
(Ⅱ)∵CF⊥BF,CF⊥AB
∴CF⊥平面ABE(8分)
∵CF∥DG
∴DG⊥平面ABE(10分)
∵DG?平面ADE
∴平面ABE⊥平面ADE(12分)
点评:本题考查直线与平面平行的判定,平面与平面垂直的判定,直线与平面所成的角,考查空间想象能力,逻辑思维能力,是中档题.

练习册系列答案
相关题目
 (2012•惠州模拟)如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB,且F是CD的中点.
(2012•惠州模拟)如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB,且F是CD的中点. (2012•枣庄一模)如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB,F为CD的中点.
(2012•枣庄一模)如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB,F为CD的中点. 如图,已知AB⊥平面ACD,DE⊥平面ACD,三角形ACD为等边三角形,AD=DE=2AB,F为CD的中点
如图,已知AB⊥平面ACD,DE⊥平面ACD,三角形ACD为等边三角形,AD=DE=2AB,F为CD的中点 如图,已知AB⊥平面ACD,DE⊥平面ACD,且AC=AD=DE=2AB=4,F为CD的中点.
如图,已知AB⊥平面ACD,DE⊥平面ACD,且AC=AD=DE=2AB=4,F为CD的中点.