题目内容
14.若f(x)=$\sqrt{tanx-\sqrt{3}}$,求函数的定义域为{x|kπ+$\frac{π}{3}$≤x<kπ+$\frac{π}{2}$,k∈Z}.分析 根据函数成立的条件即可求函数的定义域.
解答 解:要使函数有意义,则tanx-$\sqrt{3}$≥0,
即tanx≥$\sqrt{3}$,
即kπ+$\frac{π}{3}$≤x<kπ+$\frac{π}{2}$,k∈Z,
即函数的定义域为{x|kπ+$\frac{π}{3}$≤x<kπ+$\frac{π}{2}$,k∈Z},
故答案为:{x|kπ+$\frac{π}{3}$≤x<kπ+$\frac{π}{2}$,k∈Z}
点评 本题主要考查函数的定义域的求解,要求熟练掌握常见函数成立的条件.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
9.经过如图程序,变量y的值为( )
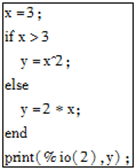
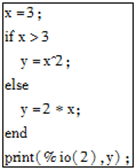
| A. | 3 | B. | 6 | C. | 9 | D. | 27 |
6.设函数f(x)在x处导数存在,则$\underset{lim}{△x→0}$$\frac{f(2)-f(2+△x)}{2△x}$=( )
| A. | -2f′(2) | B. | 2f′(2) | C. | -$\frac{1}{2}$f′(2) | D. | $\frac{1}{2}$f′(2) |