题目内容
1. 如图,在四棱锥中P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.
如图,在四棱锥中P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.(I)若PA=PD,求证:平面PQB⊥平面PAD;
(Ⅱ)若平面PAD⊥平面ABCD,PA=PD=AD=2,点M在线段PC上,且PM=2MC,求四棱锥P-ABCD与三棱锥P-QBM的体积之比.
分析 (Ⅰ)利用等腰三角形的性质可得:PQ⊥AD,利用菱形的性质与勾股定理的逆定理可得:BQ⊥AD,可得AD⊥平面PQB,即可证明.
(II)过点M作MH∥BC交PB于点H.利用面面垂直的性质定理可得:PQ⊥平面ABCD,利用四棱锥的体积计算公式可得VP-ABCD,利用面面垂直的判定定理可得:BC⊥平面PQB,于是MH⊥平面PQB,利用VP-QBM=VM-PQB即可得出.
解答 (Ⅰ)证明:∵PA=PD,Q为AD的中点,
∴PQ⊥AD,
又∵底面ABCD为菱形,∠BAD=60°,
设AB=2a,则AQ=a,从而$BQ=\sqrt{3}a$,
∴AQ2+BQ2=AB2,
∴BQ⊥AD,
又PQ∩BQ=Q,∴AD⊥平面PQB,
又AD?平面PAD,∴平面PQB⊥平面PAD;
(Ⅱ)解:过点M作MH∥BC交PB于点H.
∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,PQ⊥AD,
∴PQ⊥平面ABCD,BC?平面ABCD,
∵$PA=PD=AD=2,\;\;∴\;\;PQ=BQ=\sqrt{3}$,
∴${V_{P-ABCD}}=\frac{1}{3}PQ•{S_{菱形ABCD}}=\frac{1}{3}×\sqrt{3}×2×\sqrt{3}=2$,
∴PQ⊥BC,
又∵BQ⊥AD,AD∥BC,
∴BQ⊥BC,
又∵QB∩QP=Q,∴BC⊥平面PQB,
又∵MH∥BC,PM=2MC,∴MH⊥平面PQB,
∴$\frac{MH}{BC}=\frac{PM}{PC}=\frac{2}{3},BC=2$,
∴$MH=\frac{4}{3}$,
∴${V_{p-QBM}}={V_{M-PQB}}=\frac{1}{3}•\frac{1}{2}•\sqrt{3}•\sqrt{3}•\frac{4}{3}=\frac{2}{3}$,
∴VP-ABCD:Vp-QBM=3:1.
点评 本题考查了菱形的性质、线面面面垂直的判定与性质定理、勾股定理的逆定理、三棱锥与四棱锥的体积计算公式,考查了推理能力与计算能力,属于中档题.

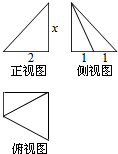
| A. | $\sqrt{13}$ | B. | $\sqrt{5}$ | C. | $\sqrt{14}$ | D. | 4 |
| A. | $\frac{7}{12}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{2}$ |
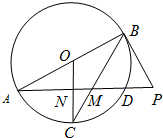 如图AB是圆O的直径,过B作圆O的切线交弦AD的延长线于点P,M为AD上一点,且PB=PM=6,PD=4,连接BM并延长交圆O于点C,连接OC交AD于点N,则CN=$\frac{{\sqrt{5}}}{2}$.
如图AB是圆O的直径,过B作圆O的切线交弦AD的延长线于点P,M为AD上一点,且PB=PM=6,PD=4,连接BM并延长交圆O于点C,连接OC交AD于点N,则CN=$\frac{{\sqrt{5}}}{2}$. 如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个焦点为F(1,0),且过点(2,0).
如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个焦点为F(1,0),且过点(2,0). 在平面直角坐标系xoy中,已知椭圆C的方程为$\frac{{x}^{2}}{8}$+y2=1,设AB是过椭圆C中心O的任意弦,l是线段AB的垂直平分线,M是l上与O不 重合的点.
在平面直角坐标系xoy中,已知椭圆C的方程为$\frac{{x}^{2}}{8}$+y2=1,设AB是过椭圆C中心O的任意弦,l是线段AB的垂直平分线,M是l上与O不 重合的点.