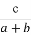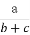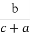题目内容
已知P(x0,y0)是抛物线y2=2px(p>0)上的一点,过P点的切线方程的斜率可通过如下方式求得:
在y2=2px两边同时求导,得:
2yy'=2p,则y'=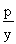 ,所以过P的切线的斜率:k=
,所以过P的切线的斜率:k=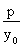 .
.
试用上述方法求出双曲线x2-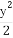 =1在P(
=1在P(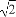 ,
,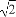 )处的切线方程为 .
)处的切线方程为 .
2x-y-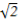 =0
=0
【解析】用类比的方法对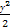 =x2-1两边同时求导得,yy'=2x,∴y'=
=x2-1两边同时求导得,yy'=2x,∴y'=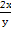 ,
,
∴y'=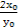 =
=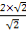 =2,
=2,
∴切线方程为y-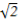 =2(x-
=2(x-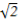 ),∴2x-y-
),∴2x-y-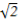 =0.
=0.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目