题目内容
已知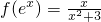 ,x∈R.
,x∈R.
(1)求f(x)的表达式;
(2)若方程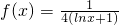 有两个不相等的实数根α,β,求αβ的值;
有两个不相等的实数根α,β,求αβ的值;
(3)若函数g(x)=f(x)-a在x∈[1,e]上有零点,求实数a的取值范围.
解:(1)令t=ex时,则x=lnt,t>0,
∵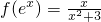 ,x∈R
,x∈R
∴ ,
,
即
(2)由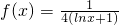 可得,3ln2x+4lnx-3=0.
可得,3ln2x+4lnx-3=0.
∵方程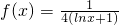 有两个不相等的实数根α,β
有两个不相等的实数根α,β
∴ ,故
,故
(3)函数g(x)=f(x)-a在[1,e]上有零点,等价于f(x)=a在(1,e]上有解.
①当x=1时,f(x)=0;
②当x∈(1,e]时,lnx∈(0,1],则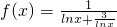 ,
,
∵lnx∈(0,1],
∴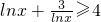 ,当且仅当lnx=1,即x=e时取等号,
,当且仅当lnx=1,即x=e时取等号,
因而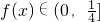 .
.
综上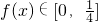 ,故
,故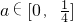
分析:解(1)令t=ex时,则x=lnt,t>0,根据
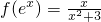 ,x∈R,可求f(x)的表达式;
,x∈R,可求f(x)的表达式;(2)由
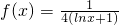 可得,3ln2x+4lnx-3=0,利用方程
可得,3ln2x+4lnx-3=0,利用方程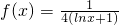 有两个不相等的实数根α,β,可得
有两个不相等的实数根α,β,可得 ,从而可求αβ的值;
,从而可求αβ的值;(3)函数g(x)=f(x)-a在[1,e]上有零点,等价于f(x)=a在(1,e]上有解.分类讨论:①当x=1时,f(x)=0;②当x∈(1,e]时,lnx∈(0,1],则
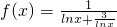 ,利用基本不等式可求
,利用基本不等式可求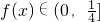 ,从而可得实数a的取值范围.
,从而可得实数a的取值范围.点评:本题以函数为载体,考查函数的解析式,考查函数与方程的关系,同时考查基本不等式的运用,解题时将函数g(x)=f(x)-a在[1,e]上有零点,转化为f(x)=a在(1,e]上有解是关键.

练习册系列答案
相关题目
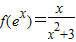 ,x∈R.
,x∈R.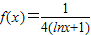 有两个不相等的实数根α,β,求αβ的值;
有两个不相等的实数根α,β,求αβ的值;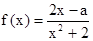 (x∈R)在区间[-1,1]上是增函数.
(x∈R)在区间[-1,1]上是增函数.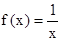 的两实数根为x1、x2,试问:是否存在实数m,使得不等式
的两实数根为x1、x2,试问:是否存在实数m,使得不等式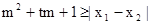 对任意a∈A及t∈[-1,1]恒成立?若存在,求出m的取值范围;若不存在,请说明理由?
对任意a∈A及t∈[-1,1]恒成立?若存在,求出m的取值范围;若不存在,请说明理由?