题目内容
3. 某商场根据甲、乙两种不同品牌的洗衣粉在周一至周五每天的销量绘成下面的茎叶图若两种品牌销量的平均数为$\overline{{x}_{甲}}$与$\overline{{x}_{乙}}$,方差为s${\;}_{甲}^{2}$与s${\;}_{乙}^{2}$,则( )
某商场根据甲、乙两种不同品牌的洗衣粉在周一至周五每天的销量绘成下面的茎叶图若两种品牌销量的平均数为$\overline{{x}_{甲}}$与$\overline{{x}_{乙}}$,方差为s${\;}_{甲}^{2}$与s${\;}_{乙}^{2}$,则( )| A. | $\overline{{x}_{甲}}$$<\overline{{x}_{乙}}$,s${\;}_{甲}^{2}$$<{s}_{乙}^{2}$ | B. | $\overline{{x}_{甲}}$$>\overrightarrow{{x}_{乙}}$,s${\;}_{甲}^{2}$$<{s}_{乙}^{2}$ | ||
| C. | $\overline{{x}_{甲}}$$>\overrightarrow{{x}_{乙}}$,s${\;}_{甲}^{2}$>s${\;}_{乙}^{2}$ | D. | $\overline{{x}_{甲}}$$<\overline{{x}_{乙}}$,s${\;}_{甲}^{2}$$>{s}_{乙}^{2}$ |
分析 根据茎叶图中的数据,计算$\overline{{x}_{甲}}$、$\overline{{x}_{乙}}$与${{s}_{甲}}^{2}$、${{s}_{乙}}^{2}$的值即可.
解答 解:根据茎叶图中的数据,得;
$\overline{{x}_{甲}}$=$\frac{1}{5}$(17+25+22+28+33)=25,
$\overline{{x}_{乙}}$=$\frac{1}{5}$(18+19+27+36+35)=27,
${{s}_{甲}}^{2}$=$\frac{1}{5}$[(17-25)2+(25-25)2+(22-25)2+(28-25)2+(33-25)2]=$\frac{146}{5}$,
${{s}_{乙}}^{2}$=$\frac{1}{5}$[(18-27)2+(19-27)2+(27-27)2+(36-27)2+(35-27)2]=$\frac{290}{5}$;
∴$\overline{{x}_{甲}}$<$\overline{{x}_{乙}}$,${{s}_{甲}}^{2}$<${{s}_{乙}}^{2}$.
故选:A.
点评 本题考查了数据的平均数与方差的应用问题,解题时可以根据公式进行计算,也可以根据定义进行估算,是基础题目.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
12.已知{an}是等差数列,{bn}是正项等比数列,若a11=b10,则( )
| A. | a13+a9=b14b6 | B. | a13+a9=b14+b6 | C. | a13+a9≥b14+b6 | D. | a13+a9≤b14+b6 |
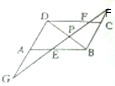 如图,四边形ABCD是平行四边形,P是BD上任意一点,过P点的直线分别交AB,DC于E,F,交DA,BC的延长线于G,H.
如图,四边形ABCD是平行四边形,P是BD上任意一点,过P点的直线分别交AB,DC于E,F,交DA,BC的延长线于G,H.