题目内容
4.已知函数f(x)=x3-3ax-1在x=-1处取得极值.(Ⅰ)求a的值;
(Ⅱ)求f(x)在[-3,2]上的最大值与最小值.
分析 (Ⅰ)先求出函数f(x)的导数,得到f′(-1)=0,解出a的值即可;
(Ⅱ)先求出函数f(x)的导数,求出函数的单调区间,从而求出函数的最值.
解答 解:(Ⅰ)f′(x)=3x2-3a=3(x2-a),
∵f(x)在x=-1处取得极大值,
∴f′(-1)=3×(-1)2-3a=0,解得:a=1;
(Ⅱ)由(Ⅰ)得:f(x)=x3-3x-1,f′(x)=3x2-3=0,解得:x=±1,
y,y′随x的变化情况如下表:
| x | -3 | (-3,-1) | -1 | (-1,1) | 1 | (1,2) | 2 |
| f′(x) | + | 0 | - | 0 | + | ||
| f(x) | -19 | 1 | -3 | 1 |
点评 本题考查了函数的单调性、最值问题,考查导数的应用,是一道基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.某程序框图如图所示,该程序运行后输出的S的值是( )
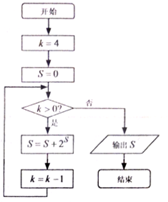

| A. | 2059 | B. | 1035 | C. | 11 | D. | 3 |
12.关于复数z=$\frac{2}{-1+i}$的四个命题:
p1:复数z对应的点在第二象限,
p2:z2=2i,
p3:z的共轭复数为1+i,
p4:z的虚部为-1.
其中的真命题个数为( )
p1:复数z对应的点在第二象限,
p2:z2=2i,
p3:z的共轭复数为1+i,
p4:z的虚部为-1.
其中的真命题个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
9.过曲线C:y=$\frac{1}{x}$(x>0)上一点P(x0,y0)作曲线C的切线,若切线的斜率为-4,则x0等于( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | 4 | D. | $\frac{1}{4}$ |