题目内容
【题目】已知函数 
（1）判断并证明函数的单调性；
（2）求此函数的最大值和最小值．
【答案】
（1）解：由题可知y= 
= 
= 
+1．
函数y= 在[3，6]上单调递减．
证明如下：
任取x1、x2∈[3，6]，不妨设x1＜x2，则 
﹣ 
= 
，
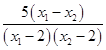由于x1﹣x2＜0，且x1﹣2＞0，x2﹣2＞0，
所以 ﹣ ＜0，即函数y= 在[3，6]上单调递减，
所以函数y= 在[3，6]上单调递减
（2）解：由（1）可知，当x=3时y取最大值 
=6，
当x=6时y取最小值 
= 
【解析】变形可知y= 
+1．（1）利用定义法判断即可；（2）结合（1）可知当x=3时y取最大值，当x=6时y取最小值，进而计算可得结论．
【考点精析】本题主要考查了函数单调性的判断方法和函数的最值及其几何意义的相关知识点，需要掌握单调性的判定法：①设x1,x2是所研究区间内任两个自变量，且x1＜x2；②判定f(x1)与f(x2)的大小；③作差比较或作商比较；利用二次函数的性质（配方法）求函数的最大（小）值；利用图象求函数的最大（小）值；利用函数单调性的判断函数的最大（小）值才能正确解答此题．
期末冲刺100分创新金卷完全试卷系列答案
【题目】某学校为了调查喜欢语文学科与性别的关系，随机调查了一些学生情况，具体数据如表：
调查统计 | 不喜欢语文 | 喜欢语文 |
男 | 13 | 10 |
女 | 7 | 20 |
为了判断喜欢语文学科是否与性别有关系，根据表中的数据，得到K2的观测值k= 
≈4.844，因为k≥3.841，根据下表中的参考数据：
P（K2≥k0） | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
判定喜欢语文学科与性别有关系，那么这种判断出错的可能性为（ ）
A.95%
B.50%
C.25%
D.5%
