题目内容
两条异面直线a，b所成的角为60°，在直线a，b上分别取点A1，E和点A，F使AA1⊥a，且AA1⊥b（称AA1为异面直线a，b的公垂线）．已知A1E=2，AF=3，EF=5，则线段AA1的长为
或3
或3
．
| 6 |
| 2 |
| 6 |
| 2 |
分析：由两条异面直线a，b所成的角为60°，AA1⊥a，且AA1⊥b，A1E=2，AF=3，EF=5，知
=
+
+
，故
2=
2+
2+
2+2
•
+2
•
+2
•
，由此能求出线段AA1的长．
| EF |
| EA1 |
| A1A |
| AF |
| EF |
| EA1 |
| A1A |
| AF |
| EA1 |
| A1A |
| A1A |
| AF |
| EA 1 |
| AF |
解答：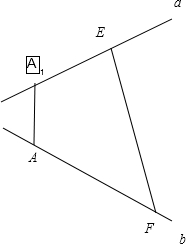
解：∵两条异面直线a，b所成的角为60°，
AA1⊥a，且AA1⊥b，A1E=2，AF=3，EF=5，
∴
=
+
+
，
∴
2=
2+
2+
2+2
•
+2
•
+2
•
，
设线段AA1的长x，
∴25=4+x2+9±2×2×3×3×cos60°，
所以x=
，或x=3
．
故答案为：
，或3
．
解：∵两条异面直线a，b所成的角为60°，AA1⊥a，且AA1⊥b，A1E=2，AF=3，EF=5，
∴
| EF |
| EA1 |
| A1A |
| AF |
∴
| EF |
| EA1 |
| A1A |
| AF |
| EA1 |
| A1A |
| A1A |
| AF |
| EA 1 |
| AF |
设线段AA1的长x，
∴25=4+x2+9±2×2×3×3×cos60°，
所以x=
| 6 |
| 2 |
故答案为：
| 6 |
| 2 |
点评：本题考查点、线、面间距离的计算，是中档题．解题时要认真审题，仔细解答，注意向量法的合理运用．易错点是忽视符号导致出错．
练习册系列答案
相关题目
已知两条异面直线a，b所成的角为
，直线l与a，直线l与b所成的角为θ，则θ的范围是（ ）
| π |
| 3 |
A、[
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
．
．
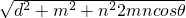