Question

已知：两条异面直线a、b所成的角为θ，它们的公垂线段AA₁的长度为d．在直线a、b上分别取点E、F，设A₁E=m，AF=n．求证：EF=．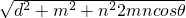

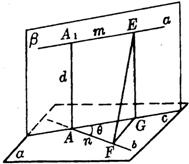Answer 1

解：设经过b与a平行的平面为α，经过a和AA₁的平面为β，α∩β=c，则c∥a．
因而b，c所成的角等于θ，且AA₁⊥c．
∵AA₁⊥b，∴AA₁⊥α．
根据两个平面垂直的判定定理，β⊥α．
在平面β内作EG⊥c，垂足为G，则EG=AA₁．
根据两个平面垂直的性质定理，EG⊥α．连接FG，则EG⊥FG．
在Rt△EFG中，EF²=EG²+FG²．
∵AG=m，∴在△AFG中，FG²=m²+n²-2mncosθ．
∵EG²=d²，∴EF²=d²+m²+n²-2mncosθ．
如果点F（或E）在点A（或A₁）的另一侧，则
EF²=d²+m²+n²+2mncosθ．
因此，EF=．
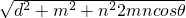分析：由题意作辅助面，作出两条异面直线a、b所成的角，再由垂直关系通过作辅助线把EF放在直角三角形中求解．
点评：本题利用条件作出辅助面和辅助线，结合线面、面面垂直的定理，在直角三角形中求公垂线的长；考查空间图形的线面关系，空间想象能力和逻辑思维能力．