题目内容
必做题, 本小题10分.解答时应写出文字说明、证明过程或演算步骤.
如图,在底面边长为1,侧棱长为2的正四棱柱 中,P是侧棱
中,P是侧棱 上的一点,
上的一点, .
.
(1)当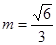 时,求直线AP与平面BDD1B1所成角的度数;
时,求直线AP与平面BDD1B1所成角的度数;
(2)在线段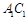 上是否存在一个定点
上是否存在一个定点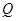 ,使得对任意的m,
,使得对任意的m,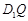 ⊥AP,并证明你的结论.
⊥AP,并证明你的结论.

【答案】
(1)60º
(2)Q为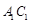 的中点时
的中点时
【解析】 (1)建立如图所示的空间直角坐标系,则
(1)建立如图所示的空间直角坐标系,则
A(1,0,0), B(1,1,0), P(0,1,m),C(0,1,0), D(0,0,0),
B1(1,1,1), D1(0,0,2).
所以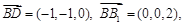

又由 的一个法向量.
的一个法向量.
设 与
与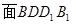 所成的角为
所成的角为 ,
,
则 =
= ,
,
解得 .故当
.故当 时,直线AP与平面
时,直线AP与平面 所成角为60º. ………5分
所成角为60º. ………5分
(2)若在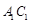 上存在这样的点Q,设此点的横坐标为x,
上存在这样的点Q,设此点的横坐标为x,
则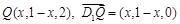 .
.
依题意,对任意的m要使D1Q在平面APD1上的射影垂直于AP. 等价于

即Q为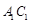 的中点时,满足题设的要求.
……………10分
的中点时,满足题设的要求.
……………10分

练习册系列答案
相关题目
 ,求直线l的斜率;
,求直线l的斜率; ,求直线l的斜率;
,求直线l的斜率; ,求直线l的斜率;
,求直线l的斜率; ,求直线l的斜率;
,求直线l的斜率;