题目内容
设数列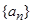 的前
的前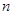 项和为
项和为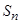 ,对任意
,对任意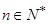 满足
满足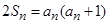 ,且
,且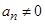 .
.
(Ⅰ)求数列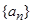 的通项公式;
的通项公式;
(Ⅱ)设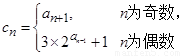 ,求数列
,求数列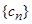 的前
的前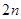 项和
项和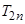 .
.
【答案】
(Ⅰ)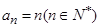 ;(Ⅱ)
;(Ⅱ)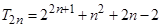 ;
;
【解析】(Ⅰ)对条件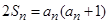 进行变形得出数列满足的递推关系,进而再求通项公式;(Ⅱ)对
进行变形得出数列满足的递推关系,进而再求通项公式;(Ⅱ)对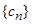 的前
的前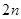 项进行分组求和,转化为等差数列和等比数列求和.
项进行分组求和,转化为等差数列和等比数列求和.
试题分析:
试题解析:(Ⅰ)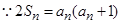 ,①
,①
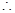 当
当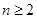 时,
时,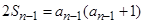 ,②
,②
以上两式相减得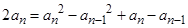 ,
2分
,
2分
即 ,
,
 ,
,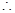 当
当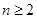 时,有
时,有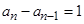 .
5分
.
5分
又当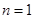 时,由
时,由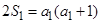 及
及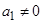 得
得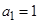 ,
,
所以数列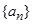 是等差数列,其通项公式为
是等差数列,其通项公式为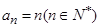 . 8分
. 8分
(Ⅱ)由(Ⅰ)得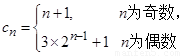 .
9分
.
9分
所以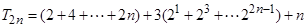 10分
10分
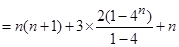
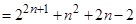 .
14分
.
14分
考点:等差数列、等比数列.

练习册系列答案
相关题目
 的前
的前 的前
的前 项和为
项和为 ,对任意的正整数
,对任意的正整数 成立,记
成立,记 。
。 的通项公式;
的通项公式; ,设数列
,设数列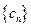 的前
的前 ,求证:对任意正整数
,求证:对任意正整数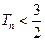 ;
; 。已知正实数
。已知正实数 满足:对任意正整数
满足:对任意正整数 恒成立,求
恒成立,求 的前
的前 项和为
项和为 ,对
,对 ,都有
,都有 成立,
成立, ,试求数列
,试求数列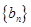 的前
的前 .
. 的前
的前 项和为
项和为 ,对一切
,对一切 ,点
,点 在函数
在函数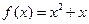 的图象上.
的图象上. 的表达式;
的表达式; ),(
),( ,
, ),(
),( ,
, ,
, ),(
),(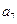 ,
,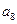 ,
, ,
, );(
);( ),(
),( ,
, ),(
),( ,
, ,
, ),(
),( ,
, ,
, ,
,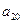 );(
);( ),…,分别计算各个括号内所有项之和,并设由这些和按原来括号的前后顺序构成的数列为
),…,分别计算各个括号内所有项之和,并设由这些和按原来括号的前后顺序构成的数列为 ,求
,求 的值;w*w^w.k&s#5@u.c~o*m
的值;w*w^w.k&s#5@u.c~o*m 为数列
为数列 的前
的前 ,使得不等式
,使得不等式 对一切
对一切