题目内容
已知
(1)若p>1时,解关于x的不等式f(x)≥0;
(2)若f(x)>2对2≤x≤4时恒成立,求p的范围.
【答案】分析:(1)对函数化简可得, ,要解不等式,需要讨论
,要解不等式,需要讨论 与-1的大小,①1<p<2②p=2时③p>2三种情况分别进行求解
与-1的大小,①1<p<2②p=2时③p>2三种情况分别进行求解
(2)由 可得x2+(p-3)x-p>0对2≤x≤4恒成立,即
可得x2+(p-3)x-p>0对2≤x≤4恒成立,即 恒成立,只要p>g(x)max,结合函数
恒成立,只要p>g(x)max,结合函数 上的单调性可求
上的单调性可求
解答:解:(1)
①
②p=2时,解集为{x|x≥-2且x≠-1}
③p>2时,解集为
(2)∵ x2+(1+p)x+p>4x+2p
x2+(1+p)x+p>4x+2p
∴x2+(p-3)x-p>0对2≤x≤4恒成立
∴ 恒成立
恒成立
∵ 上递减
上递减
∴g(x)max=g(2)=2
∴p>2
点评:本题主要考查了含有参数的不等式的求解,体现了分类讨论思想的应用,函数的恒成立与求解函数的最值的相互转化,注意函数的单调性在求解函数 最值中的应用.
 ,要解不等式,需要讨论
,要解不等式,需要讨论 与-1的大小,①1<p<2②p=2时③p>2三种情况分别进行求解
与-1的大小,①1<p<2②p=2时③p>2三种情况分别进行求解(2)由
 可得x2+(p-3)x-p>0对2≤x≤4恒成立,即
可得x2+(p-3)x-p>0对2≤x≤4恒成立,即 恒成立,只要p>g(x)max,结合函数
恒成立,只要p>g(x)max,结合函数 上的单调性可求
上的单调性可求解答:解:(1)

①

②p=2时,解集为{x|x≥-2且x≠-1}
③p>2时,解集为

(2)∵
 x2+(1+p)x+p>4x+2p
x2+(1+p)x+p>4x+2p∴x2+(p-3)x-p>0对2≤x≤4恒成立
∴
 恒成立
恒成立∵
 上递减
上递减∴g(x)max=g(2)=2
∴p>2
点评:本题主要考查了含有参数的不等式的求解,体现了分类讨论思想的应用,函数的恒成立与求解函数的最值的相互转化,注意函数的单调性在求解函数 最值中的应用.

练习册系列答案
相关题目

 ;
;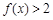 对
对 时恒成立,求p的范围.
时恒成立,求p的范围.
 ;
; 对
对 时恒成立,求p的范围.
时恒成立,求p的范围.