题目内容
已知 是由满足下述条件的函数构成的集合:对任意
是由满足下述条件的函数构成的集合:对任意 ,
,
① 方程 有实数根;② 函数
有实数根;② 函数 的导数
的导数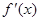 满足
满足 .
.
(Ⅰ)判断函数 是否是集合
是否是集合 中的元素,并说明理由;
中的元素,并说明理由;
(Ⅱ)集合 中的元素
中的元素 具有下面的性质:若
具有下面的性质:若 的定义域为
的定义域为 ,则对于任意
,则对于任意 ,都存在
,都存在 ,使得等式
,使得等式 成立.试用这一性质证明:方程
成立.试用这一性质证明:方程 有且只有一个实数根;
有且只有一个实数根;
(Ⅲ)对任意 ,且
,且 ,求证:对于
,求证:对于 定义域中任意的
定义域中任意的 ,
, ,
, ,当
,当 ,且
,且 时,
时,
(Ⅰ)函数 是集合
是集合 中的元素.
中的元素.
(Ⅱ)方程 有且只有一个实数根.
有且只有一个实数根.
(Ⅲ)对于任意符合条件的 ,
,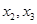 总有
总有 成立.
成立.
解析试题分析:(Ⅰ)因为①当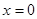 时,
时,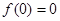 ,
,
所以方程 有实数根0;
有实数根0;
②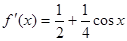 ,
,
所以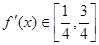 ,满足条件
,满足条件 ;
;
由①②,函数 是集合
是集合 中的元素. 5分
中的元素. 5分
(Ⅱ)假设方程 存在两个实数根
存在两个实数根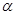 ,
,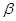
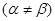 ,
,
则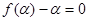 ,
,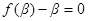 .
.
不妨设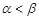 ,根据题意存在
,根据题意存在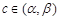 ,
,
满足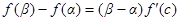 .
.
因为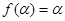 ,
,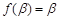 ,且
,且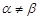 ,所以
,所以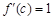 .
.
与已知 矛盾.又
矛盾.又 有实数根,
有实数根,
所以方程 有且只有一个实数根. 10分
有且只有一个实数根. 10分
(Ⅲ)当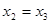 时,结论显然成立; 11分
时,结论显然成立; 11分
当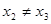 ,不妨设
,不妨设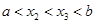 .
.
因为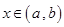 ,且
,且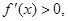 所以
所以 为增函数,那么
为增函数,那么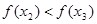 .
.
又因为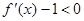 ,所以函数
,所以函数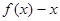 为减函数,
为减函数,
所以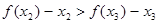 .
.
所以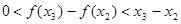 ,即
,即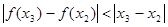 .
.
因为 ,所以
,所以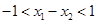 , (1)
, (1)
又因为 ,所以
,所以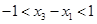 , (2)
, (2)
(1)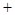 (2)得
(2)得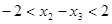 即
即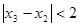 .
.
所以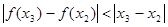
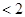 .
.
综上,对于任意符合条件的 ,
,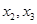 总有
总有 成立. 14分
成立. 14分
考点:本题主要考查集合的概念,函数与方程,导数研究函数单调性的应用,,反证法,不等式的证明。
点评:综合题,本题综合性较强,难度较大。证明方程只有一个实根,可通过构造函数,研究其单调性实现,本解法运用的是反证法。由自变量取值 ,且
,且 ,确定函数值的关系
,确定函数值的关系 ,关键是如何实现两者的有机转换。
,关键是如何实现两者的有机转换。

练习册系列答案
相关题目

 .
. 时①求
时①求 的单调区间;
的单调区间;  ,若对任意
,若对任意 ,存在
,存在 ,使
,使 ,求实数
,求实数 取值范围.
取值范围. 时,恒有
时,恒有 成立,求
成立,求 的取值范围.
的取值范围.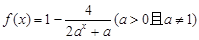 是定义在
是定义在 上的奇函数.
上的奇函数. 的值;
的值;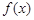 的值域;
的值域;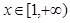 时,
时,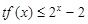 恒成立,求实数
恒成立,求实数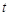 的取值范围.
的取值范围. 对于任意实数
对于任意实数 满足
满足 ,当
,当 时,
时, .
. 并判断
并判断 ,集合
,集合 ,
, ,若
,若 ,求实数
,求实数 的取值范围.
的取值范围. ,设
,设 。
。 图象上任意一点
图象上任意一点 为切点的切线的斜率
为切点的切线的斜率 恒成立,求实数
恒成立,求实数 的最小值。
的最小值。 ,使得函数
,使得函数 的图象与
的图象与 的图象恰好有四个不同的交点?若存在,求出
的图象恰好有四个不同的交点?若存在,求出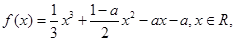 其中
其中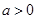 .(1)求函数
.(1)求函数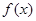 的单调区间;(2)若函数
的单调区间;(2)若函数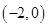 内恰有两个零点,求
内恰有两个零点,求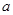 的取值范围;
的取值范围;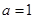 时,设函数
时,设函数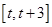 上的最大值为
上的最大值为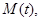 最小值为
最小值为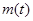 ,记
,记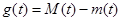 ,求函数
,求函数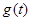 在区间
在区间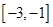 上的最小值.
上的最小值.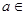 R,函数
R,函数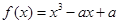 .
.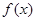 的单调区间;
的单调区间;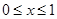 时,
时,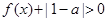 .
.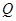 (百件)与销售价格
(百件)与销售价格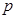 (元)的关系如下图,每月各种开支2000元.
(元)的关系如下图,每月各种开支2000元.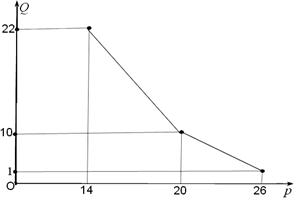
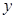 (元)与销售价格
(元)与销售价格 =
=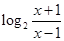 .
.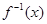 ,并求使得函数
,并求使得函数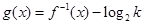 有零点的实数
有零点的实数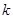 的取值范围.
的取值范围.