题目内容
在平面直角坐标系xOy中,设椭圆4x2+y2=1在矩阵A=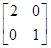 对应的变换下得到曲线F,求F的方程.
对应的变换下得到曲线F,求F的方程.
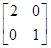 对应的变换下得到曲线F,求F的方程.
对应的变换下得到曲线F,求F的方程.x2+y2=1
设P(x0,y0)是椭圆上的任意一点,
点P(x0,y0)在矩阵A对应的变换下变为点P′(x′0,y′0),
则 =
=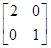
 ,∴
,∴ ∴
∴
又点P在椭圆上,∴4 +
+ =1,∴(x′0)2+(y′0)2=1,
=1,∴(x′0)2+(y′0)2=1,
∴曲线F的方程为x2+y2=1.
点P(x0,y0)在矩阵A对应的变换下变为点P′(x′0,y′0),
则
 =
=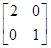
 ,∴
,∴ ∴
∴
又点P在椭圆上,∴4
 +
+ =1,∴(x′0)2+(y′0)2=1,
=1,∴(x′0)2+(y′0)2=1,∴曲线F的方程为x2+y2=1.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
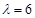 ,其对应的一个特征向量e=
,其对应的一个特征向量e=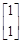 ,并且矩阵M对应的变换将点
,并且矩阵M对应的变换将点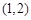 变换成点
变换成点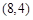 .
.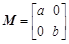 (其中
(其中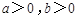 ),若曲线
),若曲线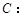
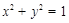 在矩阵
在矩阵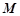 所对应的变换作用下得到曲线
所对应的变换作用下得到曲线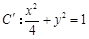 ,求
,求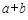 的值.
的值.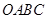 在二阶矩阵
在二阶矩阵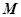 的作用下变成平行四边形
的作用下变成平行四边形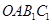 区域.
区域.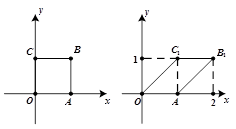
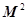 ,并判断
,并判断 .
.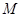 是把坐标平面上的点的横坐标伸长到3倍,纵坐标伸长到2倍的伸压变换矩阵.
是把坐标平面上的点的横坐标伸长到3倍,纵坐标伸长到2倍的伸压变换矩阵. 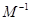 ;
;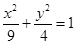 在矩阵
在矩阵 的特征多项式.
的特征多项式. =
= ,求α的值.
,求α的值.