Question

【题目】已知△ABC中，内角A，B，C所对的边分别为a，b，c，且满足asinA-csinC=b(sinA－sinB）．

（Ⅰ）求角C的大小；

（Ⅱ）若边长c=4，求△ABC的周长最大值．

Answer 1

【答案】（Ⅰ）；（Ⅱ）12.

【解析】试题分析：（1）由正弦定理把角化为边得到a2+b2-c2=ab，进而根据余弦定理即可求角；

（2）利用正弦定理将边化为角，得到a+b+c=+sinA+sin（－A），进而利用和差角公式整理得到8sin（A+）+4，利用三角函数的性质即可求解.

试题解析：

（Ⅰ）由已知，根据正弦定理，asinA-csinC=（a-b）sinB

得，a2-c2= b（a-b），即a2+b2-c2=ab．

由余弦定理得cosC==．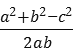

又C∈（0，π）．

所以C=．

（Ⅱ）∵C=，，A+B=，

∴，

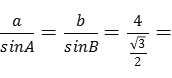
可得：a=sinA，b=sinB=sin（－A），

∴a+b+c=+sinA+sin（－A）

=+sinA+（cosA+sinA）

=8sin（A+）+4

∵由0＜A＜可知，＜A+＜，可得：＜sin（A+）≤1．

∴△ABC的周长a+b+c的最大值为12．