题目内容

已知函数f（x）=x2-5x+4，则不等式组
f(x)-f(y)≥0
1≤x≤4.
对应的平面区域为（　　）
A、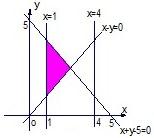精英家教网
B、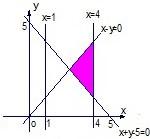精英家教网
C、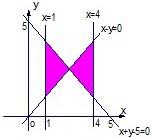精英家教网
D、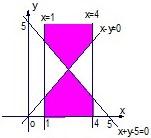精英家教网
分析：先把f（x）-f（y）≥0整理为二元一次不等式组，再由线性规划可得．
解答：解：因为f（x）=x2-5x+4，
所以f（x）-f（y）=x2-5x+4-（y2-5y+4）
=x2-y2-5（x-y）
=（x-y）（x+y-5）≥0
则
x-y≥0
x+y-5≥0
或
x-y≤0
x+y-5≤0
，
又1≤x≤4，
所以原不等式组对应的平面区域如选项C所示．
故选C．
点评：本题考查线性规划的方法及化归的思想方法．
练习册系列答案
相关题目
精英家教网已知函数f（x）=Asin（ωx+φ）（x∈R，A＞0，ω＞0，|φ|＜
π
2
）的部分图象如图所示，则f（x）的解析式是（　　）
A、f(x)=2sin(πx+
π
6
)(x∈R)
B、f(x)=2sin(2πx+
π
6
)(x∈R)
C、f(x)=2sin(πx+
π
3
)(x∈R)
D、f(x)=2sin(2πx+
π
3
)(x∈R)
（2012•深圳一模）已知函数f(x)=
1
3
x3+bx2+cx+d，设曲线y=f（x）在与x轴交点处的切线为y=4x-12，f′（x）为f（x）的导函数，且满足f′（2-x）=f′（x）．
（1）求f（x）；
（2）设g(x)=x
f′(x)
 ， m＞0，求函数g（x）在[0，m]上的最大值；
（3）设h（x）=lnf′（x），若对一切x∈[0，1]，不等式h（x+1-t）＜h（2x+2）恒成立，求实数t的取值范围．
（2011•上海模拟）已知函数f(x)=(
x
a
-1)2+(
b
x
-1)2，x∈(0，+∞)，其中0＜a＜b．
（1）当a=1，b=2时，求f（x）的最小值；
（2）若f（a）≥2m-1对任意0＜a＜b恒成立，求实数m的取值范围；
（3）设k、c＞0，当a=k2，b=（k+c）2时，记f（x）=f1（x）；当a=（k+c）2，b=（k+2c）2时，记f（x）=f2（x）．
求证：f1(x)+f2(x)＞
4c2
k(k+c)
．
已知函数f(x)=(
x
a
-1)2+(
b
x
-1)2，x∈(0，+∞)，其中0＜a＜b．
（1）当a=1，b=2时，求f（x）的最小值；
（2）若f（a）≥2m-1对任意0＜a＜b恒成立，求实数m的取值范围；
（3）设k、c＞0，当a=k2，b=（k+c）2时，记f（x）=f1（x）；当a=（k+c）2，b=（k+2c）2时，记f（x）=f2（x）．
求证：f1(x)+f2(x)＞
4c2
k(k+c)
．
已知函数f(x)=
1
3
x3+bx2+cx+d，设曲线y=f（x）在与x轴交点处的切线为y=4x-12，f′（x）为f（x）的导函数，且满足f′（2-x）=f′（x）．
（1）求f（x）；
（2）设g(x)=x
f′(x)
 ， m＞0，求函数g（x）在[0，m]上的最大值；
（3）设h（x）=lnf′（x），若对一切x∈[0，1]，不等式h（x+1-t）＜h（2x+2）恒成立，求实数t的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网