题目内容
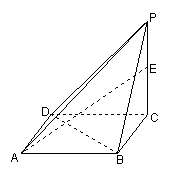
已知四棱锥P－ABCD，底面是边长为1的正方形，侧棱PC长为2，且PC⊥底面ABCD，
E是侧棱PC上的动点。
（Ⅰ） 求点C到平面PDB的距离；
（Ⅱ） 若点E为PC的中点，
求平面ADE与平面ABE所成的锐二面角的大小．
解：（1）四棱锥P－ABCD的底面是边长为1的正方形，
侧棱PC⊥底面ABCD，且PC=2. ………………2分
设点C到平面PDB的距离为d，
， 
, 
, 
---------------------------7分
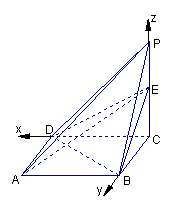
(2)以点C为坐标原点，CD所在的直线为ｘ轴建立空间直角坐标系如图示：
则
,从而
……………… 9分
设平面ADE和平面ABE的法向量分别为
由法向量的性质可得：
，
令
，则
，
∴
………12分
设二面角D－AE－B的平面角为
，则
∴ 
………………………………… 14分
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，已知四棱锥P--ABC的底面ABCD为正方形，PA⊥平面ABCD，PA=AB=2，e为PC的中点，F为AD的中点．
如图，已知四棱锥P-ABCD中，底面ABCD是直角梯形，AB∥DC，∠ABC=45°，DC=1，AB=2，PA⊥平面ABCD，PA=1．
如图，已知四棱锥P-ABCD底面ABCD为菱形，PA⊥平面ABCD，∠ABC=60°，E、F分别是BC、PC的中点．
如图，已知四棱锥P-ABCD，底面ABCD为菱形，PA⊥平面ABCD，∠ABC=60°，E、F分别是BC、PC的中点．