题目内容
(本小题满分12分)
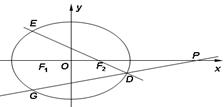
如图,已知 ,
,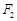 分别是椭圆
分别是椭圆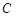 :
: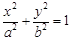 (
(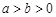 )的左、右焦点,且椭圆
)的左、右焦点,且椭圆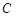 的离心率
的离心率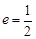 ,
, 也是抛物线
也是抛物线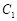 :
: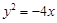 的焦点.
的焦点.
(Ⅰ)求椭圆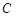 的方程;
的方程;
(Ⅱ)过点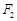 的直线
的直线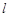 交椭圆
交椭圆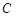 于
于 ,
,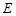 两点,
两点,
且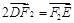 ,点
,点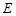 关于
关于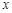 轴的对称点为
轴的对称点为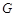 ,求直线
,求直线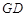 的方程.
的方程.
【答案】
解:(Ⅰ)因为抛物线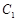 的焦点是
的焦点是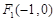 ,
,
则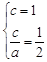 ,得
,得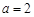 ,则
,则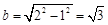 ,
,
故椭圆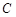 的方程为
的方程为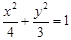 .......................................................4分
.......................................................4分
(Ⅱ)显然直线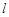 的斜率不存在时不符合题意,可设直线
的斜率不存在时不符合题意,可设直线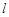 :
: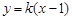 ,设
,设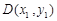 ,
,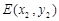 ,由于
,由于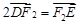 ,则
,则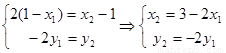 ;..........................................................6分
;..........................................................6分
联立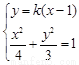 ,得
,得 ,
,
则 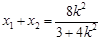 ,...........①
,...........①
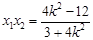 ,..............②,将
,..............②,将 代入①、②得:
代入①、②得:
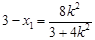 ,..............③
,..............③ 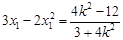 ,.....④ ,由③、④得
,.....④ ,由③、④得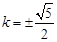 ,
,
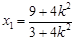
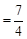 ,
,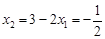 ,..................................................................................
10分
,..................................................................................
10分
(i)若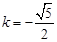 时,
时,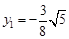 ,
,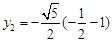
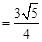 ,
,
即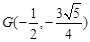 ,
,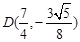 ,
,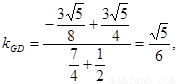 ,
,
直线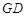 的方程是
的方程是 ;
;
(ii)当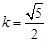 时,同理可求直线
时,同理可求直线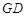 的方程是
的方程是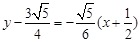 ............................12分
............................12分
【解析】略

练习册系列答案
相关题目