题目内容
【题目】已知函数f(x)=x2+2ax+2,x∈[-5,5].
求实数a的取值范围,使函数y=f(x)在区间[-5,5]上是单调函数.
【答案】(-∞,-5]∪[5,+∞)
【解析】试题分析:由二次函数对称轴与定义区间位置关系列实数a的取值条件,即-a≥5或-a≤-5,解得实数a的取值范围
试题解析:f(x)=(x+a)2+1-a2 由-a≥5 或-a≤-5 得a的范围是(-∞,-5]∪[5,+∞)

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
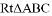 中,
中,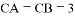 ,
,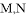 是斜边
是斜边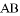 上的两个动点,且
上的两个动点,且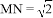 ,则
,则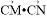 的取值范围为( )
的取值范围为( )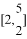 B.
B. 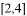 C.
C.  D.
D.