题目内容
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,过焦点
,过焦点![]() 且斜率存在的直线
且斜率存在的直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,且
两点,且![]() 点在
点在![]() 点上方,
点上方,![]() 点与
点与![]() 点关于
点关于![]() 轴对称.
轴对称.

(1)求证:直线![]() 过某一定点
过某一定点![]() ;
;
(2)当直线![]() 的斜率为正数时,若以
的斜率为正数时,若以![]() 为直径的圆过
为直径的圆过![]() ,求
,求![]() 的内切圆与
的内切圆与![]() 的外接圆的半径之比.
的外接圆的半径之比.
【答案】(1)定点![]() ;(2)
;(2)![]()
【解析】
(1)设出BD直线方程和B、D两点坐标,联立直线方程与抛物线方程,得到关于纵坐标的表达式,然后求出直线![]() 方程,继而得到定点
方程,继而得到定点
(2)求出BD、![]() 的直线方程,由点到直线距离相等求出
的直线方程,由点到直线距离相等求出![]() 内切圆半径
内切圆半径![]() ,然后求出
,然后求出![]() 的外接圆半径
的外接圆半径![]() ,得到结果
,得到结果
(1)设BD:![]() ,
,![]()
联立![]() 消x得
消x得![]()
∴![]() 恒正,
恒正,![]()
∴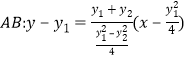 即
即![]()
令![]() ,得
,得![]()
∴定点Q![]()
(2)由题![]() =
=![]()
=![]()
∴![]() 即得
即得![]() (舍)
(舍)
∴BD:![]()
由题,![]() 的内心必在x轴上,设内心
的内心必在x轴上,设内心![]()
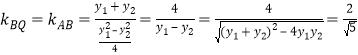
∴![]()
由I到直线BQ与到直线BD的距离相等得
![]() ,∴
,∴![]() ,内心
,内心![]()
∴![]() 内切圆半径
内切圆半径![]()
由对称性,![]() 的外心应在x轴上,设外心
的外心应在x轴上,设外心![]()
BD中垂线方程为![]() ,得
,得![]()
联立![]() 得
得![]()
∴![]() 的外接圆半径
的外接圆半径![]()
∴ ![]()

练习册系列答案
相关题目