题目内容

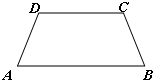（2013•长春一模）如图，等腰梯形ABCD中，AB∥CD且AB=2AD，∠DAB=
π
3
，则以A、B为焦点，且过点D的双曲线的离心率e=（　　）
分析：由题可知，双曲线离心率e=
|AB|
|DB|-|DA|
，由此可得结论．
解答：解：由题可知，双曲线离心率e=
|AB|
|DB|-|DA|
，
设|AD|=|BC|=t则|AB|=2t，|CD|=2t-2tcos60°=t，|BD|=t
5-4cos60°
=
3
t，
所以e=
|AB|
|DB|-|DA|
=
2t
3
t-t
=
3
+1，
故选B．
点评：本题考查双曲线的离心率，考查学生的计算能力，属于基础题．
练习册系列答案
相关题目
（2013•长春一模）已知：x＞0，y＞0，且
2
x
+
1
y
=1，若x+2y＞m2+2m恒成立，则实数m的取值范围是（　　）
（2013•长春一模）已知函数f（x）=ex（ax2-2x-2），a∈R且a≠0．
（1）若曲线y=f（x）在点P（2，f（2））处的切线垂直于y轴，求实数a的值；
（2）当a＞0时，求函数f（|sinx|）的最小值．
（2013•长春一模）椭圆
 x2
a2
+
y2
b2
=1(a＞b＞0)的离心率为
3
2
，右焦点到直线x+y+
6
=0的距离为2
3
，过M（0，-1）的直线l交椭圆于A，B两点．
（Ⅰ） 求椭圆的方程；
（Ⅱ） 若直线l交x轴于N，
NA
=-
7
5
NB
，求直线l的方程．
（2013•长春一模）定义在R上的函数f（x）满足f（x）+f（x+5）=16，当x∈（-1，4]时，f（x）=x2-2x，则函数f（x）在[0，2013]上的零点个数是
604
604
．
（2013•长春一模）在正项等比数列{an}中，已知a1a2a3=4，a4a5a6=12，an-1anan+1=324，则n=（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网