题目内容
(06年四川卷理)(14分)
已知函数![]() f(x)的导函数是
f(x)的导函数是![]() 。对任意两个不相等的正数
。对任意两个不相等的正数![]() ,证明:
,证明:
(Ⅰ)当![]() 时,
时,![]() ;
;
(Ⅱ)当![]() 时,
时,![]() 。
。
本小题主要考查导数的基本性质和应用,函数的性质和平均值不等式等知识及综合分析、推理论证的能力,
解析:证明:(Ⅰ)由![]()
得![]()
![]()
![]()
而![]() ①
①
又![]()
∴![]() ②
②
∵![]() ∴
∴![]()
∵![]() ∴
∴![]() ③
③
由①、②、③得
![]()
即![]()
(Ⅱ)证法一:由![]() ,得
,得![]()
∴![]()
![]()
![]()
下面证明对任意两个不相等的正数![]() ,有
,有![]() 恒成立
恒成立
即证![]() 成立
成立
∵![]()
设![]() ,则
,则![]()
令![]() 得
得![]() ,列表如下:
,列表如下:
|
|
|
|
|
|
|
|
|
| 极小值 |
|
![]() ∴
∴![]()
∴对任意两个不相等的正数![]() ,恒有
,恒有![]()
证法二:由![]() ,得
,得![]()
∴![]()
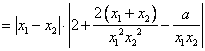
∵![]() 是两个不相等的正数
是两个不相等的正数
∴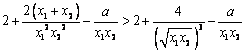
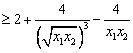
设![]() ,
,![]()
则![]() ,列表:
,列表:
|
|
|
|
|
|
|
|
|
| 极小值 |
|
∴![]() 即
即 ![]()
∴![]()
即对任意两个不相等的正数![]() ,恒有
,恒有![]()

练习册系列答案
相关题目
