题目内容
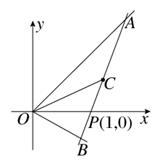
如图所示,射线OA、OB分别与x轴正半轴成45°和30°角,过点P(1,0)作直线AB分别交OA、OB于A、B两点,当AB的中点C恰好落在直线y=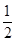 x上时,求直线AB的方程.
x上时,求直线AB的方程.
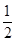 x上时,求直线AB的方程.
x上时,求直线AB的方程.
(3+ )x-2y-3-
)x-2y-3- =0.
=0.
 )x-2y-3-
)x-2y-3- =0.
=0.解:由题意可得kOA=tan45°=1,
kOB=tan(180°-30°)=- ,
,
所以射线OA的方程为y=x(x≥0),
射线OB的方程为y=- x(x≥0).
x(x≥0).
设A(m,m),B(- n,n),
n,n),
所以AB的中点C( ,
, ),
),
由点C在y=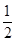 x上,且A、P、B三点共线得
x上,且A、P、B三点共线得
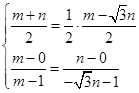
解得m= ,
,
所以A( ,
, ).
).
又P(1,0),
所以kAB=kAP= =
= ,
,
所以直线AB的方程为y= (x-1),
(x-1),
即直线AB的方程为(3+ )x-2y-3-
)x-2y-3- =0.
=0.
kOB=tan(180°-30°)=-
 ,
,所以射线OA的方程为y=x(x≥0),
射线OB的方程为y=-
 x(x≥0).
x(x≥0).设A(m,m),B(-
 n,n),
n,n),所以AB的中点C(
 ,
, ),
),由点C在y=
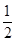 x上,且A、P、B三点共线得
x上,且A、P、B三点共线得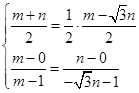
解得m=
 ,
,所以A(
 ,
, ).
).又P(1,0),
所以kAB=kAP=
 =
= ,
,所以直线AB的方程为y=
 (x-1),
(x-1),即直线AB的方程为(3+
 )x-2y-3-
)x-2y-3- =0.
=0.
练习册系列答案
相关题目
 、
、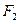 是椭圆
是椭圆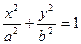 的左、右焦点,
的左、右焦点,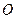 为坐标原点,点
为坐标原点,点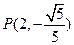 在椭圆上,线段
在椭圆上,线段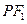 与
与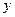 轴的交点
轴的交点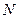 满足
满足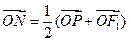 ;
;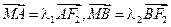 ,求
,求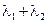 的值.
的值.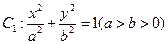 的离心率为
的离心率为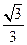 ,直线
,直线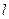 :
: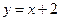 与以原点为圆心、以椭圆
与以原点为圆心、以椭圆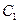 的短半轴长为半径的圆相切.
的短半轴长为半径的圆相切.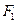 ,右焦点
,右焦点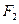 ,直线
,直线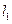 过点
过点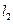 垂直
垂直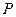 ,线段
,线段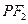 垂直平分线交
垂直平分线交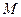 ,求点
,求点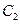 的方程;
的方程;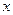 轴交于点
轴交于点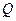 ,不同的两点
,不同的两点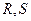 在
在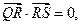 求
求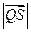 的取值范围.
的取值范围. y+2=0的倾斜角的取值范围是( )
y+2=0的倾斜角的取值范围是( )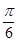 ,
,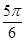 ]
]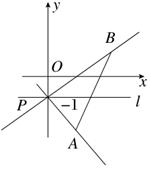
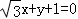 的倾斜角为( )
的倾斜角为( )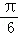
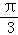
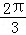
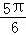
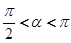 ),则直线l的倾斜角为 。
),则直线l的倾斜角为 。