题目内容
已知双曲线G的中心在原点,它的渐近线与圆x2+y2-10x+20=0相切.过点P(-4,0)作斜率为![]() 的直线l,使得l和G交于A,B两点,和y轴交于点C,并且点P在线段AB上,又满足|PA|·|PB|=|PC|2.
的直线l,使得l和G交于A,B两点,和y轴交于点C,并且点P在线段AB上,又满足|PA|·|PB|=|PC|2.
(1)求双曲线G的渐近线的方程;
(2)求双曲线G的方程;
(3)椭圆S的中心在原点,它的短轴是G的实轴.如果S中垂直于l的平行弦的中点的轨迹恰好是G的渐近线截在S内的部分AB,若P(x,y)(y>0)为椭圆上一点,求当△ABP的面积最大时点P的坐标.
解析:
|
(1)设双曲线G的渐近线的方程为y=kx, 则由渐近线与圆x2+y2-10x+20=0相切可得 所以k=± (2)由(1)可设双曲线G的方程为x2-4y2=m, 把直线 整理得3x2-8x-16-4m=0, 则xA+xB= ∵|PA|·|PB|=|PC|2,P、A、B、C共线且P在线段AB上, ∴(xP-xA)(xB-xP)=(xP-xC)2,即(xB+4)(-4-xA)=16, 整理得4(xA+xB)+xAxB+32=0.将(*)代入上式得m=28, ∴双曲线的方程为 (3)由题可设椭圆S的方程为 设垂直于 则 两式作差得 由于 所以,垂直于 又由已知,这个轨迹恰好是G的渐近线截在S内的部分,所以 故椭圆S的方程为 由题意知满足条件的P点必为平行于AB且与椭圆相切的直线m在椭圆上的切点, 易得切线m的方程为 则P点的坐标为 |

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案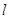 ,使得
,使得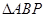 的面积最大时点P的坐标.
的面积最大时点P的坐标.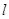 ,使得
,使得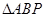 的面积最大时点P的坐标.
的面积最大时点P的坐标.