题目内容
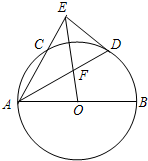（2012•武昌区模拟）（几何证明）如图，已知AB是⊙O的直径，AC是⊙O的弦，∠BAC的平分线AD交⊙O于D，过点D作DE⊥AC交AC的延长线于点E，OE交AD于点F．若| AC |
| AB |
| 3 |
| 5 |
| AF |
| FD |
| 8 |
| 5 |
| 8 |
| 5 |
分析：连接OD，BC，设AC=3k，AB=5k，BC=4k，可证OD垂直平分BC，利用勾股定理可得到OG，得到DG，于是AE=4k，然后通过OD∥AE，利用相似比即可求出
的值．
| AF |
| FD |
解答：解：连接OD，BC，如图，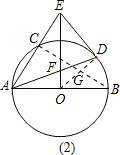
∵AB为直径，
∴∠ACB=90°，
又OD∥AE，∴∠OGB=∠ACB=90°，
∴OD⊥BC，
∴G为BC的中点，即BG=CG，
又∵
=
，
∴设AC=3k，AB=5k，根据勾股定理得：BC=
=4k，
∴OB=
AB=
，BG=
BC=2k，
∴OG=
=
，
∴DG=OD-OG=
-
=k，
又四边形CEDG为矩形，
∴CE=DG=k，
∴AE=AC+CE=3k+k=4k，
而OD∥AE，
∴
=
=
=
．
故答案为：
．
∵AB为直径，
∴∠ACB=90°，
又OD∥AE，∴∠OGB=∠ACB=90°，
∴OD⊥BC，
∴G为BC的中点，即BG=CG，
又∵
| AC |
| AB |
| 3 |
| 5 |
∴设AC=3k，AB=5k，根据勾股定理得：BC=
| AB2-AC2 |
∴OB=
| 1 |
| 2 |
| 5k |
| 2 |
| 1 |
| 2 |
∴OG=
| OB2-BG2 |
| 3k |
| 2 |
∴DG=OD-OG=
| 5k |
| 2 |
| 3k |
| 2 |
又四边形CEDG为矩形，
∴CE=DG=k，
∴AE=AC+CE=3k+k=4k，
而OD∥AE，
∴
| AF |
| FD |
| AE |
| OD |
| 4k | ||
|
| 8 |
| 5 |
故答案为：
| 8 |
| 5 |
点评：考查了与圆有关的比例线段，能够综合运用勾股定理、相似三角形的判定和性质以及平行线分线段成比例定理，属于基础题．
练习册系列答案
手拉手全优练考卷系列答案
相关题目
（2012•武昌区模拟）如图，在四棱锥P-ABCD中，底面ABCD是矩形，PA⊥平面ABCD，PA=AD，AB=
（2012•武昌区模拟）2011年武汉电视台问政直播节日首场内容是“让交通更顺畅”．A、B、C、D四个管理部门的负责人接受问政，分别负责问政A、B、C、D四个管理部门的现场市民代表（每一名代表只参加一个部门的问政）人数的条形图如下．为了了解市民对武汉市实施“让交通更顺畅”几个月来的评价，对每位现场市民都进行了问卷调查，然后用分层抽样的方法从调查问卷中抽取20份进行统计，统计结果如下面表格所示：