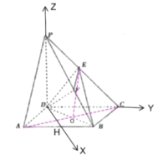
题目内容
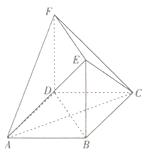
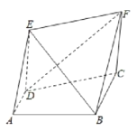
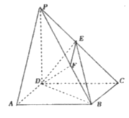
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为菱形,
为菱形,![]() ,侧棱
,侧棱![]() 底面
底面![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点,作
的中点,作![]() ,交
,交![]() 于点
于点![]() .
.
(1)求证:![]() 平面
平面![]() ;
;
(2)求证:![]() ;
;
(3)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析(2)见解析 (3)![]()
【解析】
(1)连接![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,根据中位线定理证明
,根据中位线定理证明![]() ,即可证得
,即可证得![]() 平面
平面![]() .
.
(2)先证![]() 平面
平面![]() .又∵
.又∵![]() 平面
平面![]() ,则
,则![]() .
.
(3)建立空间直角坐标系,列出各点的坐标表示,求出平面![]() 的法向量为
的法向量为![]() ,又因
,又因![]() 平面
平面![]() ,所以
,所以![]() 为平面
为平面![]() 的一条法向量,利用余弦公式求解即可得出二面角
的一条法向量,利用余弦公式求解即可得出二面角![]() 的余弦值.
的余弦值.
解:(1)证明:连接![]() 交
交![]() 于
于![]() ,连接
,连接![]() .
.
因为![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,所以
的中点,所以![]() 为
为![]() 的中位线
的中位线
∴![]() ,又
,又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]()
(2)在![]() 中,
中,![]() ,点
,点![]() 为
为![]() 的中点,
的中点,
∴ ,则
,则![]() 平面
平面![]() .
.
又∵![]() 平面
平面![]() ,则
,则![]() .
.
(3)取![]() 中点
中点![]() ,连接
,连接![]() .
.
依题意可得![]() 为等边三角形,∴
为等边三角形,∴![]() ,
,![]()
又因为![]() 底面
底面![]() ,
,![]() ,
,![]() 平面
平面![]()
则![]() ,
,![]()
建立以![]() 为坐标原点,如图所示坐标系,则有:
为坐标原点,如图所示坐标系,则有:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,设平面
,设平面![]() 的法向量为
的法向量为![]() ,
,
则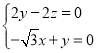
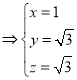 ,∴
,∴![]()
∵![]() 平面
平面![]() ,所以
,所以![]() 为平面
为平面![]() 的一条法向量,且
的一条法向量,且![]()
∴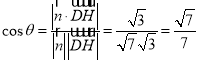

 考前必练系列答案
考前必练系列答案【题目】苹果是人们日常生活中常见的营养型水果.某地水果批发市场销售来自5个不同产地的富士苹果,各产地的包装规格相同,它们的批发价格(元/箱)和市场份额如下:
产地 |
|
|
|
|
|
批发价格 |
|
|
|
|
|
市场份额 |
|
|
|
|
|
市场份额亦称“市场占有率”.指某一产品的销售量在市场同类产品中所占比重.
(1)从该地批发市场销售的富士苹果中随机抽取一箱,求该箱苹果价格低于![]() 元的概率;
元的概率;
(2)按市场份额进行分层抽样,随机抽取![]() 箱富士苹果进行检验,
箱富士苹果进行检验,
①从产地![]() 共抽取
共抽取![]() 箱,求
箱,求![]() 的值;
的值;
②从这![]() 箱苹果中随机抽取两箱进行等级检验,求两箱产地不同的概率;
箱苹果中随机抽取两箱进行等级检验,求两箱产地不同的概率;
(3)由于受种植规模和苹果品质的影响,预计明年产地![]() 的市场份额将增加
的市场份额将增加![]() ,产地
,产地![]() 的市场份额将减少
的市场份额将减少![]() ,其它产地的市场份额不变,苹果销售价格也不变(不考虑其它因素).设今年苹果的平均批发价为每箱
,其它产地的市场份额不变,苹果销售价格也不变(不考虑其它因素).设今年苹果的平均批发价为每箱![]() 元,明年苹果的平均批发价为每箱
元,明年苹果的平均批发价为每箱![]() 元,比较
元,比较![]() 的大小.(只需写出结论)
的大小.(只需写出结论)
【题目】某公司计划购买1台机器,该种机器使用三年后即被淘汰.在购进机器时,可以一次性额外购买![]() 次维修,每次维修费用300元,另外实际维修一次还需向维修人员支付上门服务费80元.在机器使用期间,如果维修次数超过购买的
次维修,每次维修费用300元,另外实际维修一次还需向维修人员支付上门服务费80元.在机器使用期间,如果维修次数超过购买的![]() 次时,则超出的维修次数,每次只需支付维修费用700元,无需支付上门服务费.需决策在购买机器时应同时一次性购买几次维修,为此搜集并整理了100台这种机器在三年使用期内的维修次数,得到下面统计表:
次时,则超出的维修次数,每次只需支付维修费用700元,无需支付上门服务费.需决策在购买机器时应同时一次性购买几次维修,为此搜集并整理了100台这种机器在三年使用期内的维修次数,得到下面统计表:
维修次数 | 6 | 7 | 8 | 9 | 10 |
频数 | 10 | 20 | 30 | 30 | 10 |
记![]() 表示1台机器在三年使用期内的维修次数,
表示1台机器在三年使用期内的维修次数,![]() 表示1台机器维修所需的总费用(单位:元).
表示1台机器维修所需的总费用(单位:元).
(1)若![]() ,求
,求![]() 与
与![]() 的函数解析式;
的函数解析式;
(2)假设这100台机器在购机的同时每台都购买8次维修,或每台都购买9次维修,分别计算这100台机器在维修上所需总费用的平均数,并以此作为决策依据,购买1台机器的同时应购买8次还是9次维修?