题目内容
已知椭圆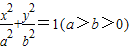 的左右焦点为F1,F2,离心率为
的左右焦点为F1,F2,离心率为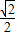 ,以线段F1 F2为直径的圆的面积为π.
,以线段F1 F2为直径的圆的面积为π.(1)求椭圆的方程;
(2)设直线l过椭圆的右焦点F2(l不垂直坐标轴),且与椭圆交于A、B两点,线段AB的垂直平分线交x轴于点M(m,0),试求m的取值范围.
【答案】分析:(1)根据离心率为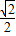 ,以线段F1 F2为直径的圆的面积为π,可求得a=
,以线段F1 F2为直径的圆的面积为π,可求得a=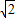 ,c=1,从而b2=1,故可求椭圆方程;
,c=1,从而b2=1,故可求椭圆方程;
(2)设出直线l的方程代入椭圆方程,从而求出线段AB的垂直平分线方程,令y=0,可得m的函数关系式,进而可求m的取值范围.
解答:解:(1)由离心率为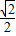 得:
得: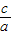 =
=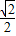 ①
①
又由线段F1 F2为直径的圆的面积为π得:πc2=π,c2=1 ②…(2分)
由①,②解得a=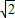 ,c=1,∴b2=1,∴椭圆方程为
,c=1,∴b2=1,∴椭圆方程为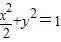 …(5分)
…(5分)
(2)由题意,F2(1,0),设l的方程为:y=k(x-1)(k≠0),代入椭圆方程为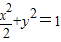
整理得(1+2k2)x2-4k2x+2k2-2=0
设A(x1,y1),B(x2,y2),AB中点为(x,y),则
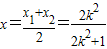 ,
,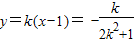
∴线段AB的垂直平分线方程为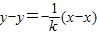
令y=0,得m=x+ky=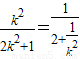
由于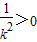 即
即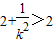 ,
,
∴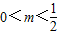 .…(13分)
.…(13分)
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,解题的关键是确定线段AB的垂直平分线方程,属于中档题.
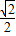 ,以线段F1 F2为直径的圆的面积为π,可求得a=
,以线段F1 F2为直径的圆的面积为π,可求得a=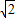 ,c=1,从而b2=1,故可求椭圆方程;
,c=1,从而b2=1,故可求椭圆方程;(2)设出直线l的方程代入椭圆方程,从而求出线段AB的垂直平分线方程,令y=0,可得m的函数关系式,进而可求m的取值范围.
解答:解:(1)由离心率为
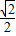 得:
得: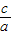 =
=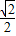 ①
①又由线段F1 F2为直径的圆的面积为π得:πc2=π,c2=1 ②…(2分)
由①,②解得a=
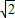 ,c=1,∴b2=1,∴椭圆方程为
,c=1,∴b2=1,∴椭圆方程为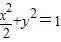 …(5分)
…(5分)(2)由题意,F2(1,0),设l的方程为:y=k(x-1)(k≠0),代入椭圆方程为
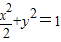
整理得(1+2k2)x2-4k2x+2k2-2=0
设A(x1,y1),B(x2,y2),AB中点为(x,y),则
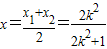 ,
,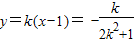
∴线段AB的垂直平分线方程为
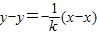
令y=0,得m=x+ky=
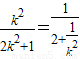
由于
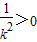 即
即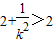 ,
,∴
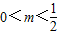 .…(13分)
.…(13分)点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,解题的关键是确定线段AB的垂直平分线方程,属于中档题.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
 的左右焦点为
的左右焦点为 ;直线
;直线 经过
经过 交椭圆于
交椭圆于 两点.
两点.
 的周长为定值.
的周长为定值. 的左右焦点为
的左右焦点为 ,直线AB过点
,直线AB过点 且交椭圆于A、B两点,则△
且交椭圆于A、B两点,则△ 的周长为_____________
的周长为_____________ 的左右焦点为
的左右焦点为 ,过点
,过点 且斜率为正数的直线
且斜率为正数的直线 交椭圆
交椭圆 于
于 两点,且
两点,且 成等差数列。
成等差数列。 与椭圆
与椭圆 两点,求使四边形
两点,求使四边形 的面积最大时的
的面积最大时的 值。
值。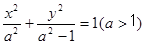 的左右焦点为
的左右焦点为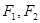 ,抛物线C:
,抛物线C: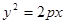 以F2为焦点且与椭圆相交于点M,直线F1M与抛物线C相切。
以F2为焦点且与椭圆相交于点M,直线F1M与抛物线C相切。 的左右焦点为F1,F2,点P-在椭圆上,若P,F1,F2是一个直角三角形的三个顶点,则点P到x轴的距离是 ( )
的左右焦点为F1,F2,点P-在椭圆上,若P,F1,F2是一个直角三角形的三个顶点,则点P到x轴的距离是 ( ) B.3 C.
B.3 C. D.
D.