题目内容
若{an}是各项均不为零的等差数列,公差为d,Sn为其前n项和,且满足
=S2n-1,n∈N*.数列{bn}满足bn=
,Tn为数列{bn}的前n项和.
(Ⅰ)求an和Tn;
(Ⅱ)若对一切正整数n,Tn≥λ•(
)n恒成立,求λ的取值范围.
| a | 2 n |
| 1 |
| an•an+1 |
(Ⅰ)求an和Tn;
(Ⅱ)若对一切正整数n,Tn≥λ•(
| 1 |
| 2 |
分析:(Ⅰ){an}是各项均不为零的等差数列,令n=1和n=2代入
=S2n-1,分别求出a1和d,求出an的通项公式,将其代入bn,利用裂项法求出其前n项和Tn;
(Ⅱ)由第一问已经求出Tn代入Tn≥λ•(
)n,可以推出λ≤
•2n,只要求出
•2n的最小值即可,从而求出λ的范围;
| a | 2 n |
(Ⅱ)由第一问已经求出Tn代入Tn≥λ•(
| 1 |
| 2 |
| n |
| 2n+1 |
| n |
| 2n+1 |
解答:解:(Ⅰ)在
=S2n-1中,
令n=1,可得a12=s1=a1,
n=2,可得a22=s3=a1+a2+a3,
∴a1=1,a22=a1+a2+a3,a1=1,
a1+a1+d+a1+2d=(a1+d)2,
解得,d=2,
从而an=a1+(n-1)×d=2n-1,…(4分)
bn=
(
-
),
于是Tn=
[(1-
)+(
-
)+…+(
-
)]=
.…(8分)
(Ⅱ)λ≤
•2n,
令cn=
•2n,
则cn+1-cn=
•2n+1-
•2n
=
•2n>0,…(12分)
于是{cn}是单调递增数列,(cn)min=c1=
,
故λ≤
.…(14分)
| a | 2 n |
令n=1,可得a12=s1=a1,
n=2,可得a22=s3=a1+a2+a3,
∴a1=1,a22=a1+a2+a3,a1=1,
a1+a1+d+a1+2d=(a1+d)2,
解得,d=2,
从而an=a1+(n-1)×d=2n-1,…(4分)
bn=
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
于是Tn=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
| n |
| 2n+1 |
(Ⅱ)λ≤
| n |
| 2n+1 |
令cn=
| n |
| 2n+1 |
则cn+1-cn=
| n+1 |
| 2n+3 |
| n |
| 2n+1 |
=
| 2n2+3n+2 |
| (2n+1)(2n+3) |
于是{cn}是单调递增数列,(cn)min=c1=
| 2 |
| 3 |
故λ≤
| 2 |
| 3 |
点评:此题主要考查等差数列的性质及其应用,第二问用到了裂项法,这是最常用的方法,关于恒成立问题,要学会转化,此题是一道中档题;

练习册系列答案
相关题目
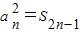 ,n∈N*.数列{bn}满足
,n∈N*.数列{bn}满足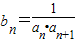 ,Tn为数列{bn}的前n项和.
,Tn为数列{bn}的前n项和.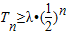 恒成立,求λ的取值范围.
恒成立,求λ的取值范围.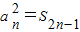 ,n∈N*.数列{bn}满足
,n∈N*.数列{bn}满足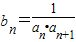 ,Tn为数列{bn}的前n项和.
,Tn为数列{bn}的前n项和.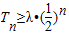 恒成立,求λ的取值范围.
恒成立,求λ的取值范围.