题目内容
例1.求下列函数的定义域(1)y=
| log0.5(log2x2+1) |
(2)y=loga[loga(logax)]
(3)y=
| 16-x2 |
分析:(1)根据偶次开方的被开方数为非负且对数函数的真数大于0可以得到:log0.5(log2x2+1)≥0,x2>0可以解出x的取值范围得到答案.
(2)由对数函数的真数大于0可以得到:loga(logax)>0,logax>0,进而求出x的取值范围得到答案.
(3)根据偶次开方的被开方数为非负且对数函数的真数大于0可以得到:16-x2≥0,sinx>0,进而求出x的取值范围得到答案.
(2)由对数函数的真数大于0可以得到:loga(logax)>0,logax>0,进而求出x的取值范围得到答案.
(3)根据偶次开方的被开方数为非负且对数函数的真数大于0可以得到:16-x2≥0,sinx>0,进而求出x的取值范围得到答案.
解答:解:(1)∵log0.5(log2x2+1)≥0,∴0<log2x2+1≤1,
又∵x2>0∴
<x≤1或-1≤x< -
故答案为:(
,1]∪[-1,-
).
(2)∵loga(logax)>0,logax>0
当a>1时,x>a,
当0<a<1时,a<x<1,
故答案为:(a,+∞)∪(a,1).
(3)∵16-x2≥0,sinx>0,
∴-4≤x≤4,2kπ<x<π+2kπ,∴-4≤x<-π,或0<x<π,
故答案为:[-4,-π)∪(0,π).
又∵x2>0∴
| ||
| 2 |
| ||
| 2 |
故答案为:(
| ||
| 2 |
| ||
| 2 |
(2)∵loga(logax)>0,logax>0
当a>1时,x>a,
当0<a<1时,a<x<1,
故答案为:(a,+∞)∪(a,1).
(3)∵16-x2≥0,sinx>0,
∴-4≤x≤4,2kπ<x<π+2kπ,∴-4≤x<-π,或0<x<π,
故答案为:[-4,-π)∪(0,π).
点评:本题主要考查求函数定义域的问题,这里要注意①偶次开方的被开方数为非负,②对数函数的真数大于0.

练习册系列答案
相关题目
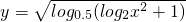 ______,
______,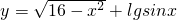 ______.
______.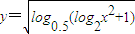 ,
,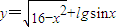 .
.