题目内容
附加题
(1)求下列函数的定义域 y=
;
(2)当x=
时,函数f(x)=(x-a1)2+(x-a2)2+…+(x-an)2取得最小值.
(1)求下列函数的定义域 y=
| 1 | ||||
1-
|
(2)当x=
| a1+a2+…+an |
| n |
| a1+a2+…+an |
| n |
分析:(1)从式子的右下角开始,逐步使式子有意义即可;
(2)由完全平方公式展开,重新整理成关于x的二次函数,进而可得答案.
(2)由完全平方公式展开,重新整理成关于x的二次函数,进而可得答案.
解答:解:(1)要使原式由意义,
则需|x|-x≠0,即x<0,
还需1-
≠0,即|x|-x≠1,解得x≠-
,
还需1-
≠0,即1-
≠1,即
≠0,
而
≠0恒成立,
综上可得,函数的定义域为:(-∞,-
)∪(-
,0);
(2)函数f(x)=(x-a1)2+(x-a2)2+…+(x-an)2
=nx2-2(a1+a2+…+an)x+a12+a22+…+an2,
由二次函数的性质可知:
当x=-
=
时,
数f(x)=(x-a1)2+(x-a2)2+…+(x-an)2取得最小值,
故答案为:
则需|x|-x≠0,即x<0,
还需1-
| 1 |
| |x|-x |
| 1 |
| 2 |
还需1-
| 1 | ||
1-
|
| 1 |
| |x|-x |
| 1 |
| |x|-x |
而
| 1 |
| |x|-x |
综上可得,函数的定义域为:(-∞,-
| 1 |
| 2 |
| 1 |
| 2 |
(2)函数f(x)=(x-a1)2+(x-a2)2+…+(x-an)2
=nx2-2(a1+a2+…+an)x+a12+a22+…+an2,
由二次函数的性质可知:
当x=-
| -2(a1+a2+…+an) |
| 2n |
| a1+a2+…+an |
| n |
数f(x)=(x-a1)2+(x-a2)2+…+(x-an)2取得最小值,
故答案为:
| a1+a2+…+an |
| n |
点评:本题考查函数定义域的求解,以及二次函数最值得求法,属基础题.

练习册系列答案
相关题目
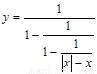
 时,函数
时,函数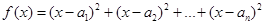 取得最小值。
取得最小值。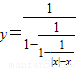 ;
;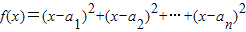 取得最小值.
取得最小值.