题目内容
平面向量 ,若存在不同时为
,若存在不同时为 的实数
的实数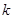 和
和 ,使
,使 且
且 ,试求函数关系式
,试求函数关系式
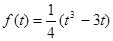
解析试题分析:由 得
得


考点:向量的数量积运算
点评:本题主要考查两个向量的数量积的运算,两个向量垂直的性质,解题的核心是计算,属于中档题.

练习册系列答案
相关题目
题目内容
平面向量 ,若存在不同时为
,若存在不同时为 的实数
的实数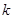 和
和 ,使
,使 且
且 ,试求函数关系式
,试求函数关系式
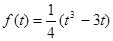
解析试题分析:由 得
得


考点:向量的数量积运算
点评:本题主要考查两个向量的数量积的运算,两个向量垂直的性质,解题的核心是计算,属于中档题.
