题目内容
9.设a为非零实数,偶函数f(x)=x2+a|x-m|+1,x∈R在区间(1,2)上只有一个零点,则实数a的取值范围为-$\frac{5}{2}$<a<-2.分析 根据函数是一个偶函数,利用偶函数的定义,写出关系式得到m的值是0,根据在区间(1,2)上存在唯一零点,得到f(1)×f(2)<0且在(1,2)上为单调函数,求出结果.
解答 解:∵f(x)=x2+a|x-m|+1是偶函数,
f(-x)=-(x)2+a|-x-m|+1,
f(x)=x 2+a|x-m|+1,
若f(x)=f(-x),
则|x+m|=|x-m|
2xm=-2xm
∴m=0
∴f(x)=x2+a|x|+1,
x∈(1,2),f(x)=x2+ax+1,若其在区间(1,2)上存在唯一零点
f(1)×f(2)<0且在(1,2)上为单调函数
∴(2+a)(5+2a)<0
∴-$\frac{5}{2}$<a<-2
故答案为:-$\frac{5}{2}$<a<-2.
点评 本题考查函数的零点的判定定理,本题解题的关键是先写出符合偶函数的定义的式子,整理出式子中的字母系数的值.

练习册系列答案
相关题目
1.棱长为a的正方体可任意摆放,则其在水平平面上投影面积的最大值为( )
| A. | $\sqrt{3}$a2 | B. | $\sqrt{2}$a2 | C. | $\frac{3\sqrt{3}}{4}$a2 | D. | 2a2 |
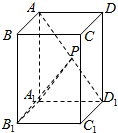 如图,已知ABCD-A1B1C1D1是底面为正方形的长方体,∠AD1A1=60°,AD1=4,点P是AD1上的动点.
如图,已知ABCD-A1B1C1D1是底面为正方形的长方体,∠AD1A1=60°,AD1=4,点P是AD1上的动点. 如图,棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD=2$\sqrt{2}$.
如图,棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD=2$\sqrt{2}$.