题目内容
18.已知点G是圆F:(x+2)2+y2=4上任意一点,R(2,0),线段GR的垂直平分线交直线GF于H.(1)求点H的轨迹C的方程;
(2)点M(1,0),P、Q是轨迹C上的两点,直线PQ过圆心F(-2,0),且F在线段PQ之间,求△PQM面积的最小值.
分析 (1)根据双曲线的定义,点H的轨迹是中心在原点,以F、R为焦点,2a=2的双曲线,即可求点H的轨迹C的方程;
(2)分类讨论,直线方程代入双曲线方程,求出面积,即可得出结论.
解答 解:(1)圆C的圆心为F(-2,0),半径r=2,|FR|=4.
连结HR,由已知得|HR|=|HG|,
∵||HF|-|HR||=||HF|-|HG||=|FG|=r=2<|FR|.
根据双曲线的定义,点H的轨迹是中心在原点,以F、R为焦点,2a=2的双曲线,
即a=1,c=2,b2=3,
∴点H的轨迹C的方程为${x}^{2}-\frac{{y}^{2}}{3}$=1…(5分)
(2)设P(x1,y1),Q(x2,y2)
若PQ⊥x轴,则直线PQ:x=-2,代入C的方程,可得y1=3,y2=-3,
S△PQM=S△PFM+S△QFM=$\frac{1}{2}×6×3$=9…(7分)
若PQ不垂直于x轴,设直线PQ:y=k(x+2)
∵F在P、Q两点之间,∴P、Q在双曲线的左支上,且y1y2<0
双曲线的渐近线为y=±$\sqrt{3}$x,|k|>$\sqrt{3}$,
y=k(x+2)与双曲线方程联立,可得(3-k2)y2-12ky+9k2=0,
∴y1y2=$\frac{9{k}^{2}}{3-{k}^{2}}$,y1+y2=$\frac{12k}{3-{k}^{2}}$,
∴|y1-y2|=6$\sqrt{1+\frac{7}{{k}^{2}-3}+\frac{12}{({k}^{2}-3)^{2}}}$>6,
∴S△PQM=$\frac{1}{2}$|y1-y2||FM|=$\frac{3}{2}$|y1-y2|>9,
综上,△PQM面积的最小值为9.
点评 本题考查点的轨迹方程的求法,考查直线与双曲线的位置关系,考查三角形面积的计算,解题时要认真审题.

 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案| A. | $\frac{\sqrt{3}}{3}$ | B. | $\sqrt{3}$ | C. | -$\frac{\sqrt{3}}{3}$ | D. | -$\sqrt{3}$ |
| A. | 11 | B. | 10 | C. | 16 | D. | 15 |
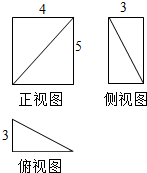
| A. | 20π | B. | 40π | C. | 50π | D. | 60π |
 如图,在平面直角坐标系xOy中,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)过点M(1,$\frac{\sqrt{2}}{2}$),离心率e=$\frac{\sqrt{2}}{2}$,F1、F2为椭圆的左、右焦点.
如图,在平面直角坐标系xOy中,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)过点M(1,$\frac{\sqrt{2}}{2}$),离心率e=$\frac{\sqrt{2}}{2}$,F1、F2为椭圆的左、右焦点. 如图,椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>0,b>0)和圆C2:x2+y2=b2,已知圆C2将椭圆C1的长轴三等分,且圆C2的面积为π,椭圆C1的下顶点为E,过坐标原点O且与坐标轴不重合的任意直线l与圆C2相交于点A、B,直线EA、EB与椭圆C1的另一个交点分别是点P、M.
如图,椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>0,b>0)和圆C2:x2+y2=b2,已知圆C2将椭圆C1的长轴三等分,且圆C2的面积为π,椭圆C1的下顶点为E,过坐标原点O且与坐标轴不重合的任意直线l与圆C2相交于点A、B,直线EA、EB与椭圆C1的另一个交点分别是点P、M.