题目内容
20.已知α,β为锐角,cosα=$\frac{1}{7}$,sin(α+β)=$\frac{5}{14}$$\sqrt{3}$,求cosβ的值及β的大小.分析 先判断0<α+β<π,求得 sinα,cos(α+β).再由cosβ=cos[(α+β)-α]求解即可,结合0<β<$\frac{π}{2}$,求得β 的值.
解答 解:∵α,β为锐角,∴0<α+β<π. …(1分)
∵cosα=$\frac{1}{7}$,sin(α+β)=$\frac{5}{14}$$\sqrt{3}$,
∴sinα=$\frac{4\sqrt{3}}{7}$,cos(α+β)=±$\frac{11}{14}$. …(4分)
当cos(α+β)=$\frac{11}{14}$时,sinβ=sin[(α+β)-α]=sin(α+β)cosα-cos(α+β)sinα=$\frac{4\sqrt{3}}{7}$×$\frac{1}{7}$-$\frac{11}{14}$×$\frac{4\sqrt{3}}{7}$<0,矛盾,
∴cos(α+β)=-$\frac{11}{14}$.…(6分)
∴cosβ=cos[(α+β)-α]=cos(α+β)cosα+sin(α+β)sinα …(8分)
=-$\frac{11}{14}$×$\frac{1}{7}$+$\frac{5\sqrt{3}}{14}$×$\frac{4\sqrt{3}}{7}$=$\frac{1}{2}$,…(10分)
又0<β<$\frac{π}{2}$,∴β=$\frac{π}{3}$.…(12分)
点评 本题主要考查同角三角函数的基本关系、两角和差的正弦、余弦公式的应用,根据三角函数的值求角,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1的内接矩形面积的最大值是( )
| A. | 16 | B. | 25 | C. | 40 | D. | 80 |
10.设集合M={x|x∈Z且-10≤x≤-3},N={x|x∈Z且|x|≤5 },则M∪N中元素的个数为( )
| A. | 11 | B. | 10 | C. | 16 | D. | 15 |
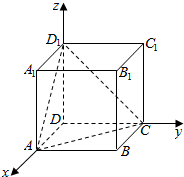 正方体ABCD-A1B1C1D1中:
正方体ABCD-A1B1C1D1中: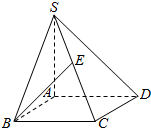 如图,在四棱锥S-ABCD中,底面是边长为2的正方形,SA⊥底面ABCD,且SA=2,E为SC的中点,则直线BE与平面ABCD所成角的正弦值为$\frac{\sqrt{3}}{3}$.
如图,在四棱锥S-ABCD中,底面是边长为2的正方形,SA⊥底面ABCD,且SA=2,E为SC的中点,则直线BE与平面ABCD所成角的正弦值为$\frac{\sqrt{3}}{3}$.