题目内容
已知函数f(x)=[x]的函数值表示不超过x的最大整数,例如:[-3.5]=-4,[2.7]=2
(1)如果实数a满足[2a+3]=3,且[3a-1]=-1,求实数a的取值范围;
(2)如果函数g(x)=x-f(x),它的定义域为(-1,3)
①求g(-0.4)和g(2.2)的值;
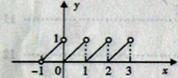
②试用分段函数的形式写出函数g(x)的解析式,并作出函数g(x)的图象.
(1)如果实数a满足[2a+3]=3,且[3a-1]=-1,求实数a的取值范围;
(2)如果函数g(x)=x-f(x),它的定义域为(-1,3)
①求g(-0.4)和g(2.2)的值;
②试用分段函数的形式写出函数g(x)的解析式,并作出函数g(x)的图象.
分析:(1)由题意,列出关于a的不等式组
,解之即可;
(2)①利用题中条件:“[x]表示不超过x的最大整数”,直接求解g(-0.4)和g(2.2)即得;
②对区间(-1,3)中的x进行分类讨论,从而求出相应的函数值即可得出函数g(x)的解析式,再分段作出函数g(x)的图象.
|
(2)①利用题中条件:“[x]表示不超过x的最大整数”,直接求解g(-0.4)和g(2.2)即得;
②对区间(-1,3)中的x进行分类讨论,从而求出相应的函数值即可得出函数g(x)的解析式,再分段作出函数g(x)的图象.
解答:解:(1)由题意,
,∴
,
即0≤a<
,
∴实数a的取值范围[0,
).
(2)①g(-0.4)=-0.4-(-1)=0.6,
g(2.2)=2.2-2=0.2,
②g(x)=
,
函数g(x)的图象如下:
|
|
即0≤a<
| 1 |
| 3 |
∴实数a的取值范围[0,
| 1 |
| 3 |
(2)①g(-0.4)=-0.4-(-1)=0.6,
g(2.2)=2.2-2=0.2,
②g(x)=
|
函数g(x)的图象如下:

点评:本小题主要考查整数、函数的值域等基础知识,考查运算求解能力、创新能力.属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|