题目内容
如图，△PAB所在的平面α和四边形ABCD所在的平面β垂直，且AD⊥α，BC⊥α，AD=4，BC=8，AB=12，∠APD=∠CPB=30°，则点P到平面β的距离是( )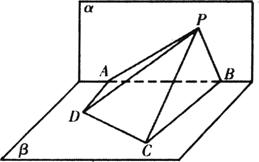
A．4
B．8 C．8
D．2
答案：A 【解析】本题考查考生分析问题、解决问题的能力以及空间想象能力、等价转化思想、空间线面关系的计算等．因为平面α⊥β,AD⊥α，∴DA⊥AP，同理CB⊥PB．即三角形ADP，CBP都是直角三角形，可以解得AP=4
，PB=8，在三角形APB中运用余弦定理，可解得∠APB=，过点P作PH⊥β，则PH为所求．
在三角形APB中运用面积公式AP·PB·sin
·12·PH
PH=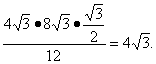
练习册系列答案
长江作业本同步练习册系列答案
相关题目
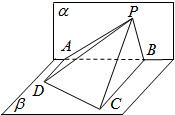如图，△PAB所在的平面α和梯形ABCD所在的平面β互相垂直，且AD⊥α，AD=4，BC=8，AB=6，若tan∠ADP+2tan∠BCP=10，则点P在平面α内的轨迹是（ ）| A、圆的一部分 | B、椭圆的一部分 | C、双曲线的一部分 | D、抛物线的一部分 |
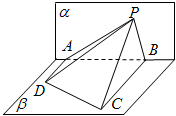如图，△PAB所在的平面α和四边形ABCD所在的平面β互相垂直，且AD⊥α，BC⊥α，AD=4，BC=8，AB=6，若tan∠ADP+2tan∠BCP=10，则点P在平面a内的轨迹是（ ）| A、圆的一部分 | B、椭圆的一部分 | C、双曲线的一部分 | D、抛物线的一部分 |
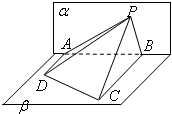如图，△PAB所在的平面α和四边形ABCD所在的平面β垂直，且AD⊥α，BC⊥α，AD=4，BC=8，AB=6，∠APD=∠CPB，则点P在平面α内的轨迹是（ ）| A、圆的一部分 | B、椭圆的一部分 | C、双曲线的一部分 | D、抛物线的一部分 |
，AD=4，
，
内的轨迹是
（ ）