题目内容
如图，△PAB所在的平面α和四边形ABCD所在的平面β垂直，且AD⊥α，BC⊥α，AD=4，BC=8，AB=6，∠APD=∠CPB，则点P在平面α内的轨迹是 ( )
A.圆的一部分 B.椭圆的一部分
C.双曲线的一部分 D.抛物线的一部分
答案：A 【解析】本题考查了立体几何与平面几何的交汇问题,圆锥曲线的轨迹的求解与判断问题.
∵∠APD=∠CPB,∴tan∠APD=tan∠CPB,即得=
,
∴
,即点P在平面α内的轨迹是圆的一部分.故应选A.
练习册系列答案
相关题目
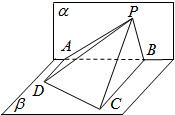如图，△PAB所在的平面α和梯形ABCD所在的平面β互相垂直，且AD⊥α，AD=4，BC=8，AB=6，若tan∠ADP+2tan∠BCP=10，则点P在平面α内的轨迹是（ ）| A、圆的一部分 | B、椭圆的一部分 | C、双曲线的一部分 | D、抛物线的一部分 |
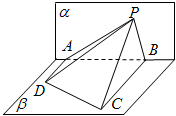如图，△PAB所在的平面α和四边形ABCD所在的平面β互相垂直，且AD⊥α，BC⊥α，AD=4，BC=8，AB=6，若tan∠ADP+2tan∠BCP=10，则点P在平面a内的轨迹是（ ）| A、圆的一部分 | B、椭圆的一部分 | C、双曲线的一部分 | D、抛物线的一部分 |
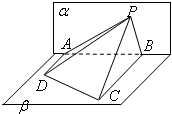如图，△PAB所在的平面α和四边形ABCD所在的平面β垂直，且AD⊥α，BC⊥α，AD=4，BC=8，AB=6，∠APD=∠CPB，则点P在平面α内的轨迹是（ ）| A、圆的一部分 | B、椭圆的一部分 | C、双曲线的一部分 | D、抛物线的一部分 |
，AD=4，
，
内的轨迹是
（ ）