题目内容
8.已知圆C过原点,圆心在射线y=2x(x>0)上,半径为$\sqrt{5}$.(1)求圆C的方程;
(2)若M为直线m:x+2y+5=0上的一动点,N为圆C上的动点,求|MN|的最小值以及|MN|取最小值时M点的坐标.
分析 (1)设圆C的方程为:(x-a)2+(y-b)2=r2.通过$\left\{{\begin{array}{l}{b=2a}\\{{a^2}+{b^2}=5}\\{a>0}\end{array}}\right.$,计算即可;
(2)通过图象可知线段MN的延长线经过圆C的圆心,且与直线m垂直时|MN|的最小,联立直线MN、m的方程,利用点到直线的距离公式计算即可.
解答 解:(1)设圆C的方程为:(x-a)2+(y-b)2=r2.
由题意知:$\left\{{\begin{array}{l}{b=2a}\\{{a^2}+{b^2}=5}\\{a>0}\end{array}}\right.$,
解得a=1,b=2.
∴圆C的方程为:(x-1)2+(y-2)2=5.
(2)由图象可知线段MN的延长线经过圆C的圆心,且与直线m垂直时|MN|的最小,
∴直线MN:y-2=2(x-1),
∵MN∩m=M,
∴联立$\left\{{\begin{array}{l}{x+2y+5=0}\\{2x-y=0}\end{array}}\right.$,得M(-1,-2),
设圆心C到直线m的距离为d,则d=$\frac{|1+4+5|}{{\sqrt{5}}}$=$2\sqrt{5}$,
∴|MN|的最小值为d-r=$\sqrt{5}$.
∴|MN|的最小值为$\sqrt{5}$,此时M的坐标(-1,-2).
点评 本题是一道直线与圆的方程的综合应用题,涉及到点到直线的距离公式等知识,注意解题方法的积累,属于中档题.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
 如图,已知点A(-4,0),AB=AC,且△ABC的内切圆方程为(x-2)2+y2=$\frac{4}{9}$.
如图,已知点A(-4,0),AB=AC,且△ABC的内切圆方程为(x-2)2+y2=$\frac{4}{9}$. 在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=1,PB=PD=$\sqrt{2}$,点E在棱PD上,且PE:ED=2:1.
在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=1,PB=PD=$\sqrt{2}$,点E在棱PD上,且PE:ED=2:1.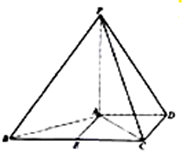 如图,已知四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥CD,
如图,已知四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥CD, 如图,在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=1.
如图,在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=1.