Question

如图，已知矩形ABCD中，AB=1，BC=a (a≥2), PA⊥平面ABCD.

100080

(1)问BC边上是否存在点Q，使得PQ⊥QD，并说明理由

 (2)若PA=1，且BC边上有且只有一个点Q，使得PQ⊥QD，求此时二面角Q—PD—A的正切值.

Answer 1

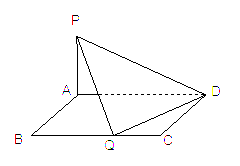
（1）存在唯 一点Q满足（2）

解析:

（1）假设存在符合条件的点Q, 连AQ, 因PA⊥平面ABCD,

则AQ是PQ在平面ABCD上的射影.由三垂线定理知

当时，因AB=1, 则以AD为直径的圆与边BC必交于

两点, 这两点满足AQ⊥DQ, 也就是说BC边上存在两个点满足

；

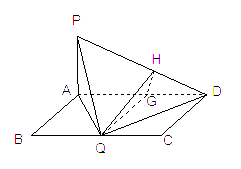当时，因AB=1, 则以AD为直径的圆与边BC相切,切点Q满足AQ⊥DQ, 即BC边上存在唯 一点Q满足；

（2）由(1)知, 此时BC=2，Q为BC中点. 因PA⊥平面ABCD, PA ?? 平面PAD, 则平面PAD⊥平面ABCD, 且平面PAD∩平面ABCD=AD.

取AD的中点G，连QG, 则QG⊥AD ?? QG⊥平面PAD,作于H, 连QH，则GH是QH在平面PAD上射影, 故是二面角Q—PD—A的平面角，在中，

，在Rt△ABC中,

即二面角Q—PD—A的正切值为.