Question

已知函数f（x）=|x|，g（x）是定义在R上的奇函数，且当x＜0时，g（x）=x（x+1），则方程f（x）+g（x）=1有

 

个实根（若有相同的实根，算一个）．

Answer 1

分析：先根据条件求出函数g（x）的解析式，原方程的实数根即 g（x）=1-f（x）的根，本题即求函数 y=g（x）和 y=1-f（x）的图象的交点个数，结合图象，得出结果．

解答：解：∵函数f（x）=|x|，g（x）是定义在R上的奇函数，且当x＜0时，g（x）=x（x+1），
设 x≥0，则-x≤0，g（-x）=-x（-x+1）=x（x-1）=-g（x），∴g（x）=x（1-x）．
综上，g（x）=

x(x+1) ，x＜0 x(1-x)  ， x≥0

，方程f（x）+g（x）=1的根，即 g（x）=1-f（x）的根，
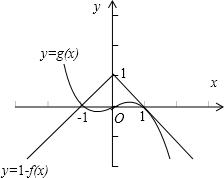
即函数 y=g（x）和 y=1-|x|的图象的交点个数，显然，两个函数的图象有2个交点，如图所示：
故答案为 2．

点评：本题考查利用函数的奇偶性求函数的解析式，方程根的个数的判断方法，体现了数形结合、转化的数学思想．