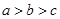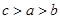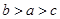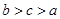题目内容
【选修4—5:不等式选讲】
已知函数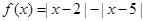 .
.
(I)求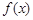 的取值范围;
的取值范围;
(II)求不等式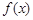 ≥
≥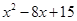 的解集.
的解集.
已知函数
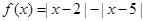 .
.(I)求
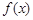 的取值范围;
的取值范围;(II)求不等式
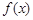 ≥
≥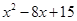 的解集.
的解集.(I) (II)不等式
(II)不等式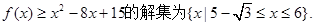
 (II)不等式
(II)不等式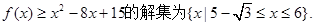
试题分析:(I)
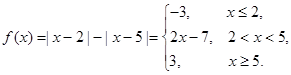
当
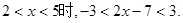
所以

(II)由(I)可知,
当
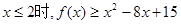 的解集为空集;
的解集为空集;当
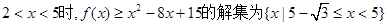 ;
;当
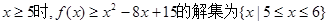 .
.综上,不等式

点评:中档题,解含绝对值不等式的基本方法,是“去绝对值符号”,思路一般有:平方法、分类讨论法或利用绝对值的几何意义。(II)分段讨论后,实际上是解一元二次不等式问题。

练习册系列答案
相关题目
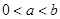 ,则下列不等式中正确的是
,则下列不等式中正确的是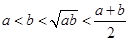


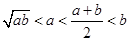
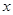 使
使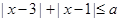 成立,则实数
成立,则实数 的取值集合是__________.
的取值集合是__________. ,则线段CD的长为________.
,则线段CD的长为________.
 :
: (t为参数)与圆C2:
(t为参数)与圆C2: (
( 为参数)的位置关系不可能是________.
为参数)的位置关系不可能是________.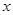 的不等式
的不等式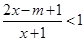 的解集为
的解集为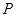 ,不等式
,不等式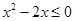 的解集为
的解集为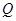 .
.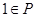 ,求实数
,求实数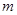 的取值范围;
的取值范围; 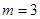 ,求集合
,求集合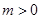 且
且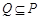 ,求
,求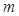 的取值范围.
的取值范围. 满足
满足 且
且 ,那么
,那么 且
且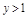
 且
且

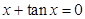 的正根从小到大地依次排列为
的正根从小到大地依次排列为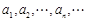 ,
,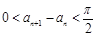 ; ②
; ②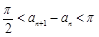 ;
;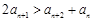 ; ④
; ④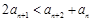 ;
;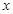 的实系数一元二次不等式
的实系数一元二次不等式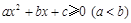 的解集为
的解集为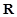 ,则
,则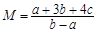 的最小值是 .
的最小值是 .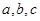 都是正数,且
都是正数,且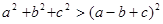
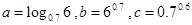 ,则
,则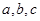 的大小关系为
的大小关系为