题目内容
已知过函数f(x)=x2的图象上点P的切线斜率为2,则点P的坐标为
- A.(-1,1)
- B.(0,0)
- C.(1,1)
- D.(2,4)
C
设点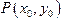 ,依题意有
,依题意有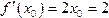 ∴
∴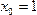 故
故
设点
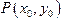 ,依题意有
,依题意有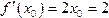 ∴
∴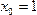 故
故

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
题目内容
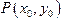 ,依题意有
,依题意有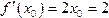 ∴
∴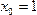 故
故

 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案