题目内容
已知过函数f(x)＝x3＋ax2＋1的图象上一点B(1，b)的切线的斜率为－3．
(1)求a，b的值；
(2)求A的取值范围，使不等式f(x)≤A－1987对于x∈[－1，4]恒成立；
(3)令g(x)＝－f(x)－3x2＋tx＋1．是否存在一个实数t，使得当x∈(0，1]时，g(x)有最大值1？
答案：
解析：
解析：
|
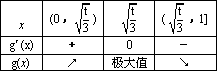
列表如下：
g( ∴t＝ ∴x＝ ③当t＜0时， ∴存在一个t＝ |
x)在x＝
处取最大值－
＋t
＝
＜3
(x)＝－3x2＋t＜0，∴g(x)在(0.1]上为减函数，不存在最大值
练习册系列答案
相关题目
，2)，则f(9)＝_________．
，
)，则k＋α＝________．
，
)，则k＋α＝
(C)2 (D)3