Question

（本小题满分12分）

   如图，直三棱柱ABC-ABC 中，AC=BC， AA=AB，D为BB的中点，E为AB上的一点，AE=3 EB

   （Ⅰ）证明：DE为异面直线AB与CD的公垂线；

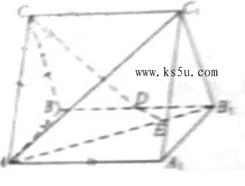   （Ⅱ）设异面直线AB与CD的夹角为45°,求二面角A-AC-B的大小

Answer 1

【解析】本题考查了立体几何中直线与平面、平面与平面及异面直线所成角与二面角的基础知识。

（1）要证明DE为AB1与CD的公垂线，即证明DE与它们都垂直，由AE=3EB1，有DE与BA1平行，由A1ABB1为正方形，可证得，证明CD与DE垂直，取AB中点F。连结DF、FC，证明DE与平面CFD垂直即可证明DE与CD垂直。

（2）由条件将异面直线AB1，CD所成角找出即为FDC，设出AB连长，求出所有能求出的边长，再作出二面角的平面角，根据所求的边长可通过解三角形求得。