题目内容
【题目】已知数列![]() 的前
的前![]() 项的和为
项的和为![]() ,记
,记![]() .
.
(1)若![]() 是首项为
是首项为![]() ,公差为
,公差为![]() 的等差数列,其中
的等差数列,其中![]() ,
,![]() 均为正数.
均为正数.
①当![]() ,
,![]() ,
,![]() 成等差数列时,求
成等差数列时,求![]() 的值;
的值;
②求证:存在唯一的正整数![]() ,使得
,使得![]() .
.
(2)设数列![]() 是公比为
是公比为![]() 的等比数列,若存在
的等比数列,若存在![]() ,
,![]() (
(![]() ,
,![]() ,
,![]() )使得
)使得![]() ,求
,求![]() 的值.
的值.
【答案】(1)①![]() ②见解析(2)
②见解析(2)![]()
【解析】
![]() 先写出
先写出![]() 的表达式.
的表达式.
![]() 写出
写出![]() ,
,![]() ,
,![]() ,列出等式求解.
,列出等式求解.
![]() 等价于
等价于![]() ,
,![]() 是一个固定的数,当
是一个固定的数,当![]() 时,区间
时,区间 互不相交,且并集为
互不相交,且并集为![]() ,所以n存在且唯一.
,所以n存在且唯一.
![]() 先将等式化成基本量表示的形式,有
先将等式化成基本量表示的形式,有![]() ,设出函数
,设出函数![]() ,当
,当![]() 时,
时,![]() ,又
,又![]() ,从而找出r,t的值,再解出q.
,从而找出r,t的值,再解出q.
(1)①因为![]() ,
,![]() ,
,![]() 成等差数列,
成等差数列,
所以![]() ,即
,即![]() ,
,
解得,![]() .
.
②由![]() ,得
,得 ,
,
整理得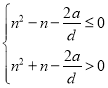 ,解得
,解得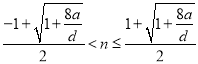 ,
,
由于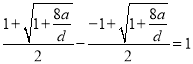 且
且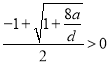 .
.
因此存在唯一的正整数![]() ,使得
,使得![]() .
.
(2)因为 ,所以
,所以![]() .
.
设![]() ,
,![]() ,
,![]() .
.
则![]() ,
,
因为![]() ,
,![]() ,所以
,所以![]() ,
,
所以![]() ,即
,即![]() ,即
,即![]() 单调递增.
单调递增.
所以当![]() 时,
时,![]() ,
,
则![]() ,即
,即![]() ,这与
,这与![]() 互相矛盾.
互相矛盾.
所以![]() ,即
,即![]() .
.
若![]() ,则
,则![]() ,
,
即![]() ,与
,与![]() 相矛盾.
相矛盾.
于是![]() ,所以
,所以![]() ,即
,即![]() .
.
又![]() ,所以
,所以![]() .
.

 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案【题目】某生物兴趣小组对冬季昼夜温差与反季节新品种大豆发芽数之间的关系进行研究,他们分别记录了![]() 月
月![]() 日至11月25日每天的昼夜温差与实验室每天100颗种子的发芽数,得到以下表格
日至11月25日每天的昼夜温差与实验室每天100颗种子的发芽数,得到以下表格
日期 | 11月21日 | 11月22日 | 11月23日 | 11月24日 | 11月25日 |
温差( | 8 | 9 | 11 | 10 | 7 |
发芽数(颗) | 22 | 26 | 31 | 27 | 19 |
该兴趣小组确定的研究方案是:先从这5组数据中选取2组数据,然后用剩下的3组数据求线性回归方程,再用被选取的![]() 组数据进行检验.
组数据进行检验.
(1)求统计数据中发芽数的平均数与方差;
(2)若选取的是11月21日与11月25日的两组数据,请根据11月22 日至11月24 日的数据,求出发芽数![]() 关于温差
关于温差![]() 的线性回归方程
的线性回归方程![]() ,若由线性回归方程得到的估计数据与所选取的检验数据的误差不超过2,则认为得到的线性回归方程是可靠的,问得到的线性回归方程是否可靠?
,若由线性回归方程得到的估计数据与所选取的检验数据的误差不超过2,则认为得到的线性回归方程是可靠的,问得到的线性回归方程是否可靠?
附:线性回归方程 中斜率和截距最小二乘估法计算公式: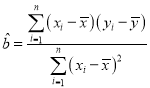 ,
,![]()
【题目】东莞的轻轨给市民出行带来了很大的方便,越来越多的市民选择乘坐轻轨出行,很多市民都会开汽车到离家最近的轻轨站,将车停放在轻轨站停车场,然后进站乘轻轨出行,这给轻轨站停车场带来很大的压力.某轻轨站停车场为了解决这个问题,决定对机动车停车施行收费制度,收费标准如下:4小时内(含4小时)每辆每次收费5元;超过4小时不超过6小时,每增加一小时收费增加3元;超过6小时不超过8小时,每增加一小时收费增加4元,超过8小时至24小时内(含24小时)收费30元;超过24小时,按前述标准重新计费.上述标准不足一小时的按一小时计费.为了调查该停车场一天的收费情况,现统计1000辆车的停留时间(假设每辆车一天内在该停车场仅停车一次),得到下面的频数分布表:
|
|
|
|
|
|
|
频数(车次) | 100 | 100 | 200 | 200 | 350 | 50 |
以车辆在停车场停留时间位于各区间的频率代替车辆在停车场停留时间位于各区间的概率.
(1)现在用分层抽样的方法从上面1000辆车中抽取了100辆车进行进一步深入调研,记录并统计了停车时长与司机性别的![]() 列联表:
列联表:
男 | 女 | 合计 | |
不超过6小时 | 30 | ||
6小时以上 | 20 | ||
合计 | 100 |
完成上述列联表,并判断能否有90%的把握认为“停车是否超过6小时”与性别有关?
(2)(i)![]() 表示某辆车一天之内(含一天)在该停车场停车一次所交费用,求
表示某辆车一天之内(含一天)在该停车场停车一次所交费用,求![]() 的概率分布列及期望
的概率分布列及期望![]() ;
;
(ii)现随机抽取该停车场内停放的3辆车,![]() 表示3辆车中停车费用大于
表示3辆车中停车费用大于![]() 的车辆数,求
的车辆数,求![]() 的概率.
的概率.
参考公式: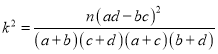 ,其中
,其中![]()
| 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.780 | 1.323 2.072 | 2.706 | 3.841 | 5.024 |