题目内容
14.已知α是三角形的内角,且sinαcosα=$\frac{1}{8}$,则cosα+sinα的值等于( )| A. | ±$\frac{5}{4}$ | B. | ±$\frac{{\sqrt{5}}}{2}$ | C. | $\frac{{\sqrt{5}}}{2}$ | D. | -$\frac{{\sqrt{5}}}{2}$ |
分析 利用三角函数的平方关系式求解即可.
解答 解:α是三角形的内角,且sinαcosα=$\frac{1}{8}$,可得α为锐角.
cosα+sinα=$\sqrt{{(cosα+sinα)}^{2}}$=$\sqrt{1+2cosα+sinα}$=$\frac{\sqrt{5}}{2}$.
故选:C.
点评 本题考查三角形的解法,三角函数的基本关系式的应用,注意角的范围是解题的关键.

练习册系列答案
相关题目
19.盘子里有肉馅、素馅和豆沙馅的包子共10个,从中随机取出1个,若它是肉馅包子的概率为$\frac{2}{5}$,它不是豆沙馅包子的概率为$\frac{7}{10}$,则素馅包子的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
6.在复平面内,复数z=$\frac{1}{1+i}+{i^3}$所对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
4.记x=log34•log56•log78,y=log45•log67•log89,则( )
| A. | x$<y<\sqrt{2}$ | B. | $\sqrt{2}$<x<y | C. | y$<\sqrt{2}$<x | D. | $\sqrt{2}$<y<x |
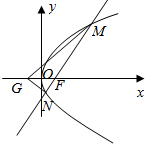 已知点F是抛物线C:y2=2px(p>0)的焦点,点A(m,2)在抛物线C上,且AF=2
已知点F是抛物线C:y2=2px(p>0)的焦点,点A(m,2)在抛物线C上,且AF=2