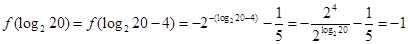题目内容
定义在R上的函数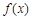 满足
满足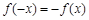 ,
,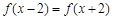 ,且
,且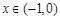 时,
时,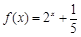 则
则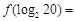 __________
__________
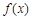 满足
满足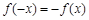 ,
,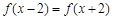 ,且
,且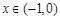 时,
时,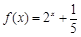 则
则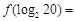 __________
__________-1
因为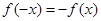 ,所以
,所以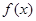 是奇函数,所以当
是奇函数,所以当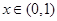 时,
时,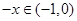 ,则
,则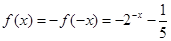
因为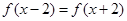 ,所以
,所以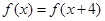 ,所以
,所以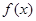 是周期为4的周期函数。而
是周期为4的周期函数。而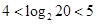 ,所以
,所以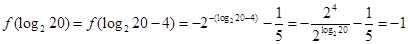
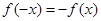 ,所以
,所以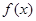 是奇函数,所以当
是奇函数,所以当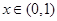 时,
时,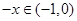 ,则
,则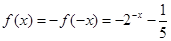
因为
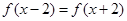 ,所以
,所以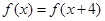 ,所以
,所以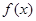 是周期为4的周期函数。而
是周期为4的周期函数。而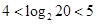 ,所以
,所以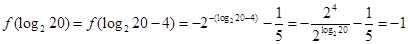

练习册系列答案
相关题目
题目内容
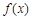 满足
满足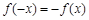 ,
,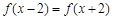 ,且
,且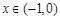 时,
时,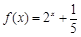 则
则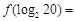 __________
__________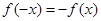 ,所以
,所以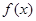 是奇函数,所以当
是奇函数,所以当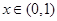 时,
时,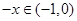 ,则
,则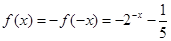
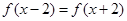 ,所以
,所以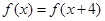 ,所以
,所以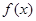 是周期为4的周期函数。而
是周期为4的周期函数。而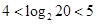 ,所以
,所以