题目内容
命题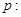 关于
关于 的不等式
的不等式 对一切
对一切 恒成立;命题
恒成立;命题 函数
函数 是减函数,若
是减函数,若 为真命题,
为真命题, 为假命题,则实数
为假命题,则实数 的取值范围为 .
的取值范围为 .
【答案】
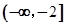
【解析】
试题分析:本题先求出命题p,q为真命题时实数a的取值范围,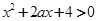 对一切
对一切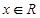 恒成立,则
恒成立,则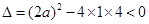 ,解得
,解得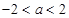 ,即命题
,即命题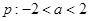 ;函数
;函数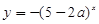 是减函数,则
是减函数,则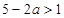 ,得
,得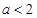 ,即命题
,即命题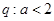 .
.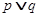 为真命题,则
为真命题,则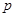 和
和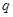 至少有一个为真,
至少有一个为真,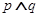 为假命题,则
为假命题,则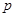 和
和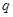 至少有一个为假,所以
至少有一个为假,所以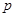 和
和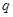 一真一假,但本题中
一真一假,但本题中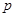 为真时,
为真时,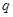 一定为真,故
一定为真,故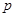 假且
假且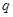 真,∴实数
真,∴实数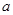 的取值范围是
的取值范围是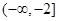 .
.
考点:逻辑连接词.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
| 下列命题: ①设函数f(x)=g(x)+x2,曲线y=g(x)在点(1,g(1))处的切线方程为y=2x+1,则曲线y=f(x)在点(1,f(1))处切线的斜率为-
②关于x的不等式(a-3)x2<(4a-2)x对任意的a∈(0,1)恒成立,则x的取值范围是(-∞,-1]∪[
③变量X与Y相对应的一组数据为(10,1),(11.3,2),(11.8,3),(12.5,4),(13,5);变量U与V相对应的一组数据为(10,5),(11.3,4),(11.8,3),(12.5,2),(13,1),r1表示变量Y与X之间的线性相关系数,r2表示变量V与U之间的线性相关系数,则r2<0<r1; ④下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据
以上命题正确的个数是( ) |